 |
  |
|||||
 |
 |
 |
 |
 |
 |
|
  |
||||||
THREE WORLDS OF MATHEMATICS
The theory of three worlds of mathematics is now formulated in detail in the book How Humans Learn to Think Mathematically. This offers a framework for the development of mathematical thinking based on perception developing subtly in sophistication through the mental world of conceptual embodiment, operation developing through actions that become mathematical operations in a world of operational symbolism and increasingly subtle use of verbal reason that leads to formal aspects of embodiment and symbolism and eventually to a world of axiomatic formalism. The development takes account of the individual's previous experience which may operate successfully in one context yet remain supportive or become problematic in another, giving rise to emotional reactions to mathematics, leading to a spectrum of success and failure over the longer term. The book starts with the newborn child and traces the development of mathematical thinking throughout school, university and on to the frontiers of research.
Recent published paper summarizing the ideas
My whole life in mathematics education has been devoted to understanding the growth of mathematics at all ages with differing individuals. In my research, I found three fundamentally different ways of operation, one through physical and mental embodiment, including action and the use of visual and other senses, a second through the use of mathematical symbols that operate as process and concept (procepts) in arithmetic, algebra and symbolic calculus, and a third using formal language in increasingly sophisticated formal mathematics in advanced mathematical thinking. As I considered the whole range of mathematical thinking, I began to realise that the notion of three different worlds of mathematics:
offered a useful categorisation for different kinds of mathematical context. Each has its own individual style of cognitive growth, each has a different way of using language and together they cover a wide range of mathematical activity. An outline of the origins of the theory can be found here and more information (published in For the Learning of Mathematics, 2004) here.
Specific applications of the theory in different contexts are also available: in calculus/analysis given in Rio de Janiero, the Overheads for a recent talk in Bogota, the role of the three different worlds in proof from a presentation in Taipei, and a paper on the three different worlds for the concept of vector, with Anna Watson and Takis Spirou.
Further developments of the theory are reported in presentations given on mathematical learning from childhood to adulthood and the transition from embodiment and symbolism to formal proof. Several invited keynotes for different international audiences are below.
Over time the framework has been developed to take into account genetic aspects which are 'set-before' our birth and cognitive development building experiences 'met-before' in one's development.
The three major set-befores are:
recognition (of similarities, differences and patterns) that may be categorised to give new thinkable concepts,
repetition (of sequences of actions) that may be routinised into automatic procedures,
language, that enables categorisation of thinkable concepts, encapsulation of actions as symbols that can act flexibly as process to do or concept to think about and definition of mathematical structures in a formal sense.
These set-befores lead to the development of each of the three worlds of mathematics which grow more sophisticated and interconnected as the individual matures.
For many learners, algebra only gets as far as the use of procedural techniques (e.g. Lima & Tall, 2008) which show little sign of flexibility in the meaning of symbols as process and concept. Instead, the symbols are 'shifted around' in a way which we term 'procedural embodiment' which involves an imagined movement of symbols, accompanied by a touch of 'magic' to get the right answer (for instance, 'move the term to the other side of the equation and change its sign').
In the later years of secondary school, the introduction of definitions in geometry and the 'rules of arithmetic' in algebra' can lead to formal embodiment in geometry and formal symbolism in arithmetic and algebra, giving a framework as follows:
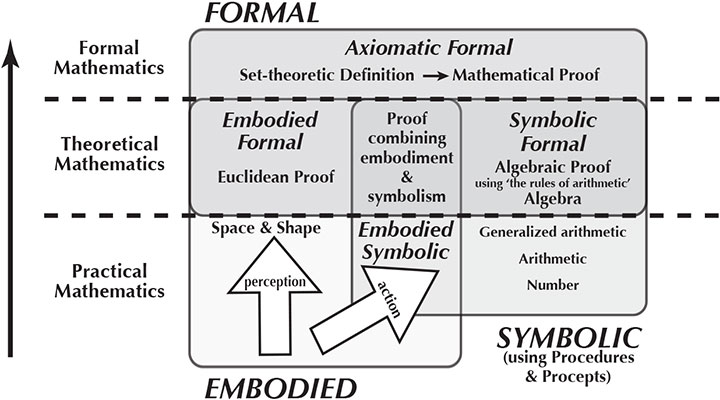
The whole framework has now been published the book How Humans Learn to Think Mathematically.
More recent developments contributing to the theoretical framework include the role of emotion (2010c), the effects of previous experience (supportive and problematic met-before (2010b), and the unifying notion of crystalline concept (2011a).
Selected papers on The Three Worlds of Mathematics:
2002j Anna Watson (and David Tall), (2002). Embodied action, effect, and symbol in mathematical growth. In Anne D. Cockburn & Elena Nardi (Eds), Proceedings of the 26th Conference of the International Group for the Psychology of Mathematics Education, 4, 369–376. Norwich: UK.
2002k David Tall, (2002). Differing Modes of Proof and Belief in Mathematics, International Conference on Mathematics: Understanding Proving and Proving to Understand, 91–107. National Taiwan Normal University, Taipei, Taiwan.
2003a Watson, A., Spirou, P., Tall, D. O. (2003). The Relationship between Physical Embodiment and Mathematical Symbolism: The Concept of Vector. The Mediterranean Journal of Mathematics Education. 1 2, 73-97.
2003a David Tall (2003). Using Technology to Support an Embodied Approach to Learning Concepts in Mathematics, First Coloquio de Historia e Tecnologia no Ensino de Matemática, at Universidade do Estado do Rio De Janeiro, February 21-3, 2002. pp. 1–28.
2004a Introducing Three Worlds of Mathematics. For the Learning of Mathematics. A response to comments about 'the three worlds' including a discussion on the building of theories.
2004b Thinking Through Three Worlds of Mathematics.Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, Bergen, Norway, 4, 281–288. An introduction to the origins and ideas in ‘the three worlds‘.
2005e David Tall (2005). A Theory of Mathematical Growth through Embodiment, Symbolism and Proof. Plenary Lecture for the International Colloquium on Mathematical Learning from Early Childhood to Adulthood, Belgium, 5-7 July 2005. A description of the framework of development from child to adult, starting from foundational principles.
2005f David Tall (2005). The transition from embodied thought experiment and symbolic manipulation to formal proof. Plenary Lecture for the Delta Conference, Frazer Island, Australia, November 2005. [An analysis of the transition from conceptual embodiment and proceptual symbolism to formal proof.]
2006b David Tall (2006). A life-time’s journey from definition and deduction to ambiguity and insight. Retirement as Process and Concept: A Festschrift for Eddie Gray and David Tall, Prague. 275-288, ISBN 80-7290-255-5. [A celebration of those who have taught me almost everything I know.]
2006h David Tall & Juan Pablo Mejia-Ramos (2006)
. The Long-Term Cognitive Development of Different Types of Reasoning and Proof, presented at the Conference on Explanation and Proof in Mathematics: Philosophical and Educational Perspectives, Essen, Germany. (pre-publication draft).
2007f Eddie Gray & David Tall (2007). Abstraction as a natural process of mental compression. Mathematics Education Research Journal, 19 ( 2), 23–40.
2008e David Tall (2008). The Transition to Formal Thinking in Mathematics. Mathematics Education Research Journal, 2008, 20 (2), 5-24
2009x David Tall (2009). Cognitive and social development of proof through embodiment, symbolism & formalism. ICMI Conference on Proof.
2010b Mercedes McGowen & David Tall (2010). Metaphor or Met-before? The effects of previous experience on the practice and theory of learning mathematics. Journal of Mathematical Behavior 29, 169–179.
2010d David Tall (2010). Perceptions, Operations and Proof in Undergraduate Mathematics, CULMS Newsletter (Community for Undergraduale Learning in the Mathematical Sciences), University of Auckland, New Zealand, 2, November 2010, 21-28.
2011a David Tall (2011) Crystalline concepts in long-term mathematical invention and discovery. For the Learning of Mathematics. January 2011.
Some recent keynote talks focusing of different aspects of the theory:
2006h David Tall (2006). Encouraging Mathematical Thinking that has both power and simplicity. Plenary presented at the APEC-Tsukuba International Conference, December 3–7, 2006, at the JICA Institute for International Cooperation (Ichigaya, Tokyo). [The overall framework of three worlds of mathematics for an audience interested in elementary school teaching, concentrating on the relationship between embodiment and symbolism.]
2007b David Tall (2007). Embodiment, Symbolism and Formalism in Undergraduate Mathematics Education, Plenary at 10th Conference of the Special Interest Group of the Mathematical Association of America on Research in Undergraduate Mathematics Education, Feb 22–27, 2007, San Diego, California, USA. [A presentation to an audience interested in undergraduate mathematics education, concentrating on the relationship between embodiment and symbolism in school and the formalism of definition-theorem-proof.] [Overheads]
2007c David Tall (2007). Teachers as Mentors to encourage both power and simplicity in active mathematical learning. Plenary at The Third Annual Conference for Middle East Teachers of Science, Mathematics and Computing, 17–19 March 2007, Abu Dhabi. [A presentation to secondary mathematics teachers, focusing on the relationship between embodiment and symbolism and the need for teachers to take into account ideas of compression of knowledge and what students bring to their studies.]
2007d Embodiment, Symbolism, Argumentation and Proof, Keynote presented at the Conference on Reading, Writing and Argumentation at National Changhua Normal University, Taiwan, May 2007.
2007e Setting Lesson Study within a long-term framework of learning. Presented at APEC Conference on Lesson Study in Thailand, August 2007.
For more recent papers, see my downloads page.
|
last modified: |