 |
  |
|||||
COGNITIVE DEVELOPMENT
My interests in cognitive development in mathematics have matured over the years. Initially, as a mathematics lecturer at university, seeing mathematics through the eyes of a mathematician, I used mathematical theories (such as catastrophe theory) to formulate cognitive theory. After researching concepts of limits and infinity, I designed computer software to visualize calculus ideas using the idea of 'local straightness' rather than formal limits, and expanded my interest in visualization. Working first with Michael Thomas on algebra, then Eddie Gray on arithmetic, I was able to see the links between symbolism in arithmetic, algebra and calculus. This led directly to the theory of procepts which is concerned essentially with symbols that represent both process and concept and the ability to switch flexibly between processes 'to do' and concepts 'to think about'. Eddie and I were then able to see what we termed 'the proceptual divide '- the bifurcation between those children who remain focused on more specific procedures rather than develop the flexibility of proceptual thinking.
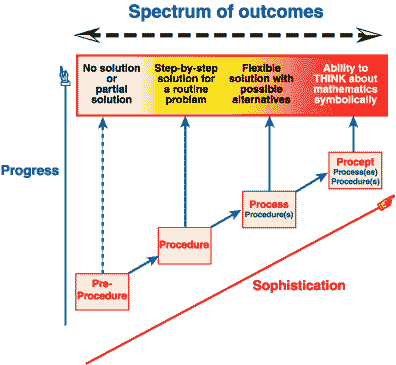
The cognitive theory developed to integrate visual and symbolic aspects and their eventual transformation into axiomatic definition and proof in advanced mathematical thinking. It is a simple theory based on perception, action and reflection, which is capable of giving insight into why some individuals are successful in mathematics but many others find it increasingly difficult.

Perception, Action and Reflection in Mathematical Growth (from 2001a, below)
EARLY IDEAS FROM A MORE MATHEMATICAL VIEWPOINT
1976a Conflicts and catastrophes in the learning of mathematics, Mathematical Education for Teaching 2,4 2-18.
1977a Cognitive conflict in the learning of mathematics, paper presented at the first meeting of the International Group for the Psychology of Learning Mathematics, Utrecht, Holland.
1978a The dynamics of understanding mathematics, Mathematics Teaching, 81, 50-52.
1978b Mathematical Thinking and the Brain, Osnabrücker Schriften zür Mathematik, 333-343.
1979e Qualitative thought processes in clinical interviews, Proceedings of the Third International Conference for the Psychology of Mathematics Education, Warwick, 206-207.
1980e The anatomy of a discovery in mathematical research, For the Learning of Mathematics, 1, 2 25-30.
DEVELOPING A COGNITIVE THEORY
1981a (with Shlomo Vinner) Concept image and concept definition in mathematics, with special reference to limits and continuity, Educational Studies in Mathematics, 12 151-169.
1988e Concept Image and Concept Definition, Senior Secondary Mathematics Education, (ed. Jan de Lange, Michiel Doorman), OW&OC Utrecht, 37-41.
1996b A Versatile Theory of Visualisation and Symbolisation in Mathematics, Plenary Presentation, Proceedings of the 46th Conference of CIEAEM, Toulouse, France (July, 1994), 1, 15-27.
1995b Mathematical Growth in Elementary and Advanced Mathematical Thinking, plenary address. In L. Meira & D. Carraher, (Eds.), Proceedings of PME 19, Recife, Brazil, I, 61-75.
APPLYING AND EXTENDING THE THEORY
1996c Can all children climb the same curriculum ladder?, The Mathematical Ability of School Leavers, Gresham College, London, 23-32.
1996d (with Robin Foster), Can all children climb the same curriculum ladder?, Mathematics in School, 25 3,8-12.
1996e (with Maselan bin Ali), Procedural and Conceptual Aspects of Standard Algorithms, Proceedings of PME 20, Valencia, 2, 19-26.
1997c (with Garry Davis & Michael Thomas), What is the object of the encapsulation of a process?, In F. Biddulph & K. Carr (Eds.) People in Mathematics Education, MERGA 20, Aotearoa. 2,132-139, MERGA Inc.
1997e (with Eddie Gray & Demetra Pitta), The Nature of the Object as an Integral Component of Numerical Processes, Proceedings of PME 21, Finland, 1, 115-130.
1999c Reflections on APOS theory in Elementary and Advanced Mathematical Thinking. In O. Zaslavsky (Ed.), Proceedings of the 23rd Conference of PME, Haifa, Israel, 1, 111-118.
1999k (with Eddie Gray, Demetra Pitta, Marcia Pinto), Knowledge Construction and diverging thinking in elementary and advanced mathematics, Educational Studies in Mathematics, 38 (1-3), 111-133.
2000a (with Michael Thomas, Garry Davis, Eddie Gray, Adrian Simpson), What is the object of the encapsulation of a process?, Journal of Mathematical Behavior, 18 (2), 1-19.
2000b (with Eddie Gray, Demetra Pitta), Objects, Actions And Images: A Perspective On Early Number Development. Journal of Mathematical Behavior,18, 4, 1-13.
2001a (with Eddie Gray, Maselan Bin Ali, Lillie Crowley, Phil DeMarois, Mercedes McGowen, Demetra Pitta, Marcia Pinto, Michael Thomas, and Yudariah Yusof). Symbols and the Bifurcation between Procedural and Conceptual Thinking, Canadian Journal of Science, Mathematics and Technology Education 1, 80-104.
2001i (with Eddie Gray) Relationships between embodied objects and symbolic procepts: an explanatory theory of success and failure in mathematics, Proceedings of PME 25.
LATEST THEORETICAL DEVELOPMENTS
The notion of THREE WORLDS OF MATHEMATICS (see separate entry).
The role of previous experience in terms of supportive and problematic met-befores (2010b)
The role of emotion in terms of Skemp's theory of goals and anti-goals. (2010c)
The unifying notion of crystalline concept (2011a).
|
last modified: |