My research focuses on the development of numerical methods and mathematical tools to analyse stochastic systems. Applications include fluid dynamics and turbulence, atmosphere and ocean dynamics, and biological and chemical systems. My work concentrates on the prediction of pathways and rates of occurrence of rare and extreme events in realistic complex systems, to develop numerical methods for their simulation, and to quantify the effects of random perturbations on the system's long term behavior.
Projects
Samplepath large deviations: Numerics and Theory
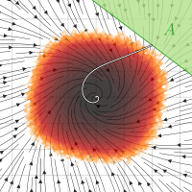
Rare but extreme events in complex systems can often efficiently be described by samplepath large deviations: In the limit of some smallness-parameter approaching zero (such as temperature for chemical reactions, inverse number of particles for thermodynamic limits, or inverse timescale separation for multiscale systems), probabilities and most likely pathways of occurrence can be readily accessible. For large and strongly coupled stochastic systems, such as climate, atmosphere, or ocean, the corresponding computations pose a huge numerical challenge. These methods borrow heavily from field theory, and represent the rare probability as a path integral, necessitating the computation of instantons and fluctuation determinants. In this project, we address these challenges, including (1) how to compute the large deviation minimizer (instanton) for large systems, (2) how to compute next-order prefactor corrections, and (3) how to deal with heavy-tailed distributions
Multistable climate regimes
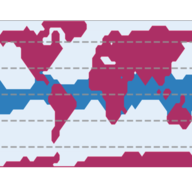
Earth's climate is a highly complex, non-equilibrium and chaotic stochastic system. In this project, we attempt to classify its chaotic attractors with methods from non-equilibrium statistical mechanics, large deviation theory and manifold learning. Concretely, due to the ice albedo feedback, the climate is known to exist in two locally stable states, the current (warm) climate, and a "snowball" state, where the globe is covered in ice. Some models even suggest additional metastable climate states, such as the slushball Earth. Transitions between these climate states, and their local stability, can in principle be analyzed in light of the non-equilibrium quasipotential, characterizing the expected transition times and most likely escape paths out of the current climate state.
Stability of Atmospheric Jets
Atmospheric flows on rotating planets are prone to form jets that are surprisingly stable in time. This behaviour can be predicted by simulating the planet's atmosphere numerically. In certain parameter regimes, the underlying dynamical system has multiple locally stable solutions, corresponding to atmosphere configurations with different numbers of jets. This project explores the mechanisms by which random turbulent fluctuations in the atmosphere drive the system to transition between these fixed points, effectively creating or destroying atmospheric jets in the process.
Large Deviations for Rogue Waves
In this project, Rogue Waves in deep sea are investigated using the modified nonlinear Schrödinger (MNLS) equation in one spatial-dimension with random initial conditions. The initial conditions approximate realistic conditions of a uni-directional sea state, taken as the JONSWAP spectrum. It is shown that one can use the incomplete information contained in this spectrum as prior and supplement this information with the MNLS dynamics to reliably estimate the probability distribution of the sea surface elevation far in the tail at later times. The Rogue Wave events encountered in numerical simulations, as well as in experiments in a 270m wave channel in Norway, agree with their most likely (instanton) configuration obtained from the theory.
Metastability in Active Matter: Motile Microorganisms
Active materials can self-organize in many more ways than their equilibrium counterparts. For example, self-propelled particles whose velocity decreases with their density can display motility-induced phase separation (MIPS), a phenomenon building on a positive feedback loop in which patterns emerge in locations where the particles slow down. Here, we investigate the effects of intrinsic fluctuations in the system's dynamics on MIPS. We show that these fluctuations can lead to transitions between metastable patterns. The pathway and rate of these transitions is analyzed within the realm of large deviation theory, and they are shown to proceed in a very different way than one would predict from arguments based on detailed-balance and microscopic reversibility.
Simple Geometric Minimum Action
Small random perturbations may have a dramatic impact on the long time evolution of dynamical systems, and large deviation theory is often the right theoretical framework to understand these effects. At the core of the theory lies the minimization of an action functional, which in many cases of interest has to be computed by numerical means. Here, a numerical method is presented to effectively compute minimizers of the Freidlin-Wentzell action functional in very general settings. The matlab source code of the algorithm and some test problems is available for download.
Instantons for Fluid Turbulence
Rare but extreme events are known to have dramatic influence on the statistics of turbulent flows, but are notoriously hard to handle both analytically and numerically. As alternative approach methods borrowed from field theory, most notably the instanton approach, allow for a direct computation of the most probable realizations of extreme events that dominate turbulent statistics. Not only can it be shown that the extreme events predicted by instanton analysis actually appear in turbulent flows, but we can furthermore predict the tail scaling of PDFs of turbulent quantities.
Adaptive Mesh Refinement and High Performance Computing
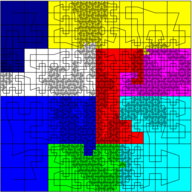
In order to integrate partial differential equations from fluid dynamics at extremely high resolution, a numerical framework has been developed to obtain high precision solutions using an adaptive grid that increases the numerical resolution locally as needed. This framework is usable on massively parallel machines and shows close-to-optimal scaling on up to \(10^5\) CPUs.
Finite Time Singularities in the Euler equations
There has been a history of claims for and against possible numerical evidence for a finite-time singularity of the incompressible three-dimensional Euler equations. Addressing the shortcomings of simply monitoring peak vorticty to discern a singularity, this project aims to instead numerically test the assumptions posed by analytic blowup criteria connecting geometric properties of Lagrangian vortex line segments, like curvature and spreading, to possible finite-time singular behavior.