Tobias Grafke — Metastability in Active Matter: Transitions between Colony Patterns in Reproducing Motile Microorganisms

Summary: Active materials can self-organize in many more ways than their equilibrium counterparts. For example, self-propelled particles whose velocity decreases with their density can display motility-induced phase separation (MIPS), a phenomenon building on a positive feedback loop in which patterns emerge in locations where the particles slow down. Here, we investigate the effects of intrinsic fluctuations in the system's dynamics on MIPS. We show that these fluctuations can lead to transitions between metastable patterns. The pathway and rate of these transitions is analyzed within the realm of large deviation theory, and they are shown to proceed in a very different way than one would predict from arguments based on detailed-balance and microscopic reversibility.

Introduction

Bacteria show complex collective behaviour. For example, bacteria such as E. Coli

are capable of active propulsion, i.e. have a free-swimming (planktonic) stage.
hey are capable of sensing their environment through quorum sensing, density-dependent gene regulation.
They stick to surface to form biofilms, high density colonies.
They exhibit cyclic/time-periodic behaviour: Biofilm formation, maturation, dispersion, planktonic stage.

The goal of this project is as follows:

Main Problem: Is it possible to describe similarly complex life-cycles as emergent behaviour of a large number of simple individual agents subject to a small number of collective rules?

Continuum description of motile bacteria

We model the motion of motile reproducing microorganisms with simple behavioural rules. The self-propulsion is modelled as active Brownian motion. For position $X\in\Omega\subset\mathbb{R}^d$, direction $\hat n \in S^{d-1}$, and location dependent swim speed $v(X)\in\mathbb{R}$

$$\dot X = v(X) \hat{n}\,,$$

$$d\hat n = \tau^{-1/2} P\circ dW\,,\qquad P=\textrm{Id} - \hat n \hat n^T$$

The direction vector diffuses on $S^{d-1}$ with tumbling rate $\tau^{-1}$. The fast tumlbing limit $\tau\to0$ yields Brownian motion

$$ dX = \sqrt{2 D(X)} \circ dW $$

with density dependend diffusivity $D(x) = v^2(x)$. Now consider $N$ such particles with position $X_i, i\in\{1,\dots,N\}$. To model quorum sensing, introduce scale $\delta$ over which particles feel each other's influence,

$$dX_i = \sqrt{2 D(\rho_{N,\delta}(t,X_i))}\circ dW_i$$

with

$$\rho_{N,\delta}(t,x) = \int_\Omega \phi_\delta(x-y)\rho_N(t,y)\,dy,\qquad \rho_N(t,x) = \frac1N \sum_{j=1}^N \delta(x-X_j(t))$$

In the limit $N\to\infty$, through a Deans-type argument, this yields a closed integro-differential equation for $\rho_N\to\rho$,

$$\partial_t \rho = \nabla\cdot(D(\rho_\delta) \nabla\rho +\tfrac12 D'(\rho_\delta)\nabla \rho_\delta),\qquad \rho_\delta(t,x) = \int_\Omega \phi_\delta(x-y)\rho(t,x) \,dy$$

in the sense that

$$\forall\ \varepsilon,T>0:\quad \lim_{N\to\infty} \mathcal P\Big(\sup_{0\le t\le T}\Big| \frac1N \sum_{j=1}^N f(X_j(t))-\int_\Omega \rho(t,x) f(x)\,dx \Big| >\varepsilon \Big)=0$$

To make this model closed in $\rho(t,x)$, consider $D(\rho)=D_0 e^{-\rho}$, and expand in $\delta\ll1$,

$$\rho_\delta(x) \approx \rho(x) + \tfrac12 \delta^2 \partial_x^2 \rho(x)\,.$$

Then we obtain an effective diffusion equation

$$\partial_t \rho = \nabla \cdot (D_e(\rho)\nabla\rho - \delta^2 \rho D(\rho) \nabla\Delta \rho)$$

with diffusivity

$$ D_e(\rho) = D(\rho) + \tfrac12 D'(\rho)\rho\,. $$

Despite the microscopic model being not reversible, the continuum model restores detailed balance

$$ \partial_t\rho = \nabla\cdot(\rho D(\rho) \nabla(\delta E/\delta \rho)) $$

with free energy

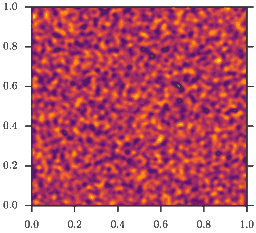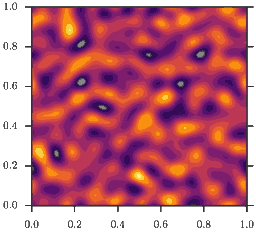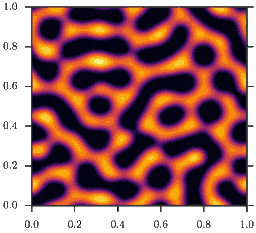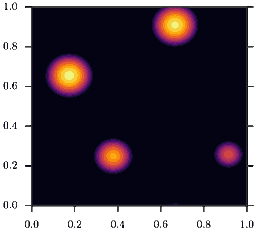
$$ E(\rho) = \int_\Omega (\rho\log\rho - \rho + f(\rho) + \tfrac12 \delta^2 |\nabla \rho|^2)\,dx\,,\quad f'(\rho)=\tfrac12 \log D(\rho) $$

In other words, the model is a $(\rho D(\rho))$-Wasserstein gradient flow. This model demonstrates the effect of motility induced phase separation: While the microscopic diffusivity $D(\rho)$ is strictly positive, this is no longer true for the effective diffusivity $D_e(\rho)$! For example, for $D(\rho) = D_0 e^{-\rho}$, the effective diffusivty becomes

$$D_e(\rho) = D_0 (1-\tfrac12\rho) e^{-\rho}$$

As a consequence, homogeneous configurations $\rho(x) = \bar\rho$ are only stable, if $\bar\rho<2$. If instead $\bar\rho>2$ phase separation occurs, as depicted in the animation. This is the mentioned feedback loop: Accumulation induced slowdown and slowdown-induced accumulation.

We now additionally introduce a second behavioral rule for the active agents: Reproduction and competition. This is models as a Poisson process

$$A\stackrel{\lambda_r}{\longrightarrow} A+A\qquad\lambda_r=\alpha\qquad\text{(reproduction)}$$

$$A+A\stackrel{\lambda_c}{\longrightarrow} A\qquad\lambda_c=\alpha/\rho_0\qquad\text{(competition)} $$

with carrying capacity $\rho_0$ and timescale $\alpha$. In the limit $N\to\infty$, this effectively leads to logistic growth

$$\partial_t \rho = \nabla \cdot (D_e(\rho)\nabla\rho - \delta^2 \rho D(\rho) \nabla\Delta \rho) {\color{red} + \alpha \rho (1-\rho/\rho_0)} $$

Interestingly, now, phase separation will eventually occur if $D_e(\rho_0)<0$, even if currently $D_e(\bar\rho)>0$. In other words, the system will drive itself into instability. In particular, we identify three regimes, with spinodal density $\rho_S$ and critical density $\rho_c$:

if $\rho_0 < \rho_S$, only the homogeneous solution will be stable, and no instability occurs (homogeneous phase)
if $\rho_S < \rho_0 < \rho_c$, instead limit cycles occur, where reproduction induces motility induced phase separation, but the resulting dense bacterial clusters are unsustainable under the current carrying capacity, and thus slowly die out.
if $\rho_c < \rho_0$, bacterial clusters become (meta-)stable.

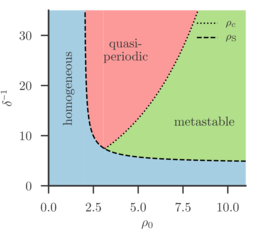
This behavior is reminiscient of the biofilm-planktonic lifecycle: Bacteria occur in a diluted planctonic phase, until a critical density is reached. They then stick to walls to form a biofilm, which over time slowly dissolves back into the planktonic phase. The corresponding phase-diagram in carrying capacity $\rho_0$ and inverse quorum sensing range (equivalently, domain-size), $\delta^{-1}$, is shown in the figure.

Relevant publications

T. Grafke, M. Cates, and E. Vanden-Eijnden, "Spatiotemporal Self-Organization of Fluctuating Bacterial Colonies", Phys. Rev. Lett. 119 (2017), 188003 (link)