Summary: In order to integrate partial differential equations from fluid dynamics at extremely high resolution, a numerical framework has been developed to obtain high precision solutions using an adaptive grid that increases the numerical resolution locally as needed. This framework is usable on massively parallel machines and shows close-to-optimal scaling on up to \(10^5\) CPUs.
In fluid dynamics, physical features are often localised. In particular in a setup such as in this project, highly detailed flow structures are clustered in a very small region, while the majority of the computational domain is filled with relatively harmless flow. Yet, due to the non-local nature of incompressible fluids, even far-away parts of the flow may have important impact locally. In such a case, adaptive mesh refinement, as introduced in the pioneering work of Berger and Colella (J. Comp. Phys., 82, 64, 1989), is a natural choice.
In the implementation presented here, based on the numerical framework racoon II, a block-structured adaptive mesh refinement is used: The computational domain is devided into equally sized blocks. Whenever a chosen refinement threshold is exceeded, a block is subdevided into \(2^d\) child blocks, where \(d\) is the domain dimension. Similarly, child blocks are merged when the threshold is no longer exceeded. The resulting octree-structure allows the grid to adaptively follow the computationally expensive structures, while remaining relatively simple: To the program, regardless of the position and resolution, each block locally looks identical. Its dimensions may be optimized, for example, towards hardware requirements such as the cache size. This provides performance-advantages over the usually more flexible patch-based or unstructured refinement techniques.
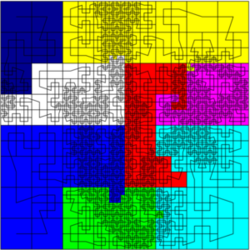

Above, a snapshot of a simulation of a Rayleigh-Taylor instability is shown as example, color denoting the fluid density. The blocks of the grid, shown on the right, follow the physical structure of the flow, resolution is highest at points where the gradients get large.
Parallelization is achieved by distributing the blocks among the available processors by traversing a space-filling Hilbert curve. This not allows for a mapping between the block octree-structure to a linear processor number, but optimizes for locality of the blocks: Blocks lying close together in the computational domain have a high probability of also being close along the Hilbert curve and thus tend to reside on the same compute node. This is depicted on the left of the above figures, where color denotes the processor ID.
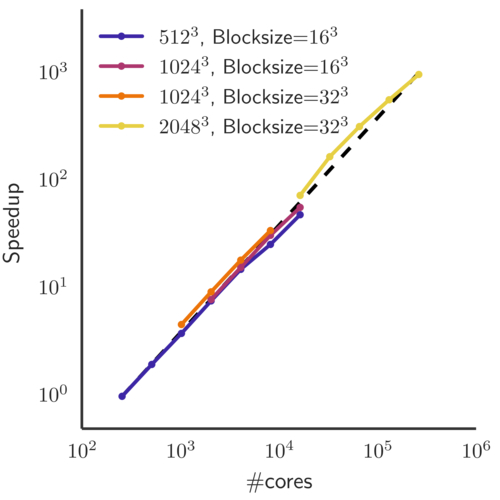
The computational framework can be used to solve three-dimensional partial differential equations for hydro-dynamics or magneto-hydro-dynamics on massively parallel machines. The above figure shows the parallel scaling (mixed weak and strong) up to \(\approx 2\cdot10^5\) CPUs. Up to this number, the scaling is close to optimal: Doubling the computational ressources roughly halves the amount of time the computation takes.
Relevant publications
-
T. Grafke, H. Homann, J. Dreher and R. Grauer, "Numerical simulations of possible finite time singularities in the incompressible Euler equations: comparison of numerical methods", Physica D 237 (2008), 1932
-
T. Grafke, "Finite-time Euler Singularities: A Lagrangian perspective", PhD thesis (Jun 2012)