Most plastics, when you stretch them, stretch, neck, and then break. However, certain plastics undergo a stress oscillation as they are stretched, the cause of which is unknown. For example, figure 1 shows a picture of light and dark patterns caused by the stress oscillation when stretching PET (PolyEthyleneTerephthalate), taken from figure 3 of Bazhenov (2011). A more 3D view of the same effect is shown in figure 2, taken from figure 3 of Ronkay & Czigány (2006). A movie of this process is shown in figure 3, taken from the supplementary material of Wan et al (2018). A stress–strain plot of the resulting oscillations is shown in figure 4, taken from figure 2a of Bazhenov & Kechekyan (2002).

Figure 1. Undeformed (left) and deformed (right) PET plastic, with the instability giving rise to light and dark bands. From figure 3 of Bazhenov (2011).

Figure 2. Photograph showing undeformed PET plastic (top) and deformed PET plastic (bottom), with the instability giving rise to light and dark bands. From figure 3 of Ronkay & Czigány (2006).

Figure 3. Stretching a PBS plastic dogbone sample at a constant strain rate. Video taken from Wan et al (2018).

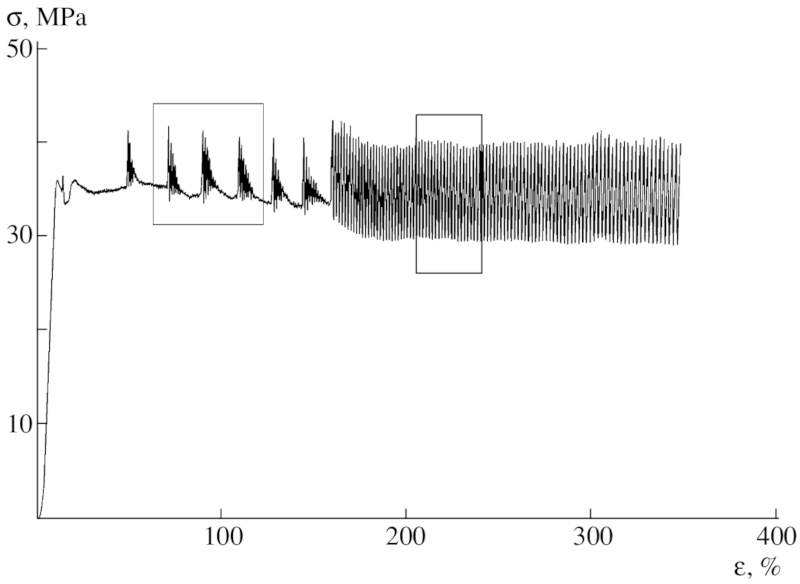
Figure 4. Stress–strain plot of uniaxial extension of PET plastic, showing two different types of instabilities. From figure 2a of Bazhenov & Kechekyan (2002).

A number of papers have tried to investigate why this banding pattern happens, including some rather rudimentary mathematical models. However, all the mathematical models so far are wrong! The best bet so far appears to be the model by Toda (1994) (see also Toda et al 2002). These studies are limited to a draw ratio of λ=2, which is not realistic, whilst more recent attempts to generalize these models (e.g. Bazhenov 2011) do not conserve mass. I also have doubts over the accuracy with which Toda (1994) numerically solved their model.

This project looks at building a simple mathematical model of the stretching plastic that is not so wrong, and then simulating that model on a computer (using, for example, Matlab), to see how realistically the model performs. The project builds on work by Seamus Stinson (2019) performed over during an Undergraduate Research Summer Studentship at Warwick.

This is a theory heavy project, and so an interest and liking for pen-and-paper mathematics and scientific computing (Matlab, Python, etc) is required. Knowledge of any of the following would be helpful, but is not necessary, as these could be learnt during the project:

• simulating differential equations (for example, using finite differences, or finite volume);
• elasticity and plasticity; and
• the material science of plastics.