Research (Out of Date)
The great virtue of studying a simple model analytically rather than solving a more complicated one numerically is that it places the understanding of a phenomenon on a sound footing. This in turn makes it possible to extrapolate with some confidence to related problems in which exact analysis is impossible.
Sound in a curved intake
Figure 1 shows a typical curved aircraft engine intake, such as might be found on a military aircraft (this intake is actually the standard RAE 2129 inlet diffuser test case). Air enters the intake at a Mach number of 0.5, and enters the curved section of the duct on the left of the figure. The fan of the engine would be just off the right hand side of the curved section.
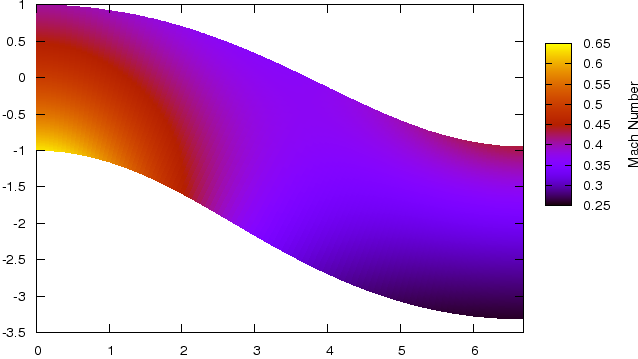
On top of this steady flow, there are unsteady perturbations (e.g. sound), which we consider to be small and so we can linearize about the steady flow. We also make use of the fact the the geometry of the intake varies slowly along it's length, and so we can use the method of Multiple Scales. This work extends the results of Rienstra[2] to allow for a strongly-curved centreline.
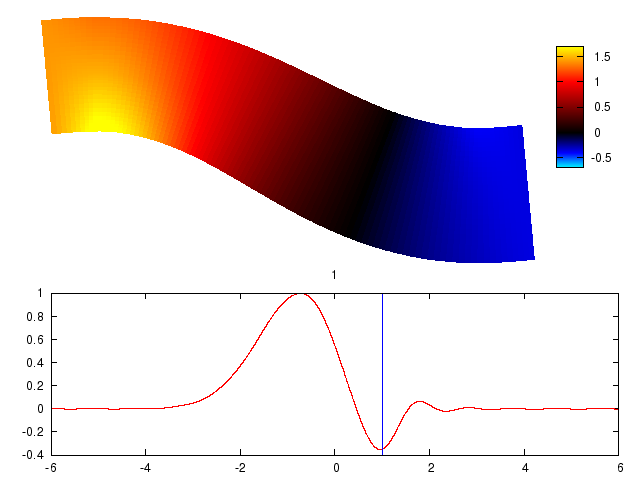
Figure 2 shows a pulse being emitted from the engine fan (the right of the duct) and then travelling upstream along the duct (to the left). The bottom graph shows the pulse that is emitted from the engine, with the vertical line showing the current time. The top graph shows the pressure of the pulse. Red is an increase in pressure and blue is a decrease. Yellow and cyan show an amplification of pressure due to the duct geometry. A movie of this is also available:
Shocks in a curved intake
If the unsteady perturbations are not small, nonlinear effects occur; for example, wavefront steepening and potentially the formation of shock waves. This can be seen in figure 3, generated by a simple 2D numerical model. The smooth pulse shown in figure 2 is fed into the right hand side, and shocks midway though the intake. A movie of this is also available.

The notable feature of of this is that the shock front remains planar. Although the front is not always normal to the duct centreline, nonetheless it exits the curved section as a plane shock without any reflection or mutation due to the curved section. The suggest that a one-dimensional mathematical model may be able to predict this, at least qualitatively. This is current work in progress.
- Movie ( 0.6MB, 800x216)
Wiener–Hopf scattering
Figure 4 shows, on the left, a cylindrical duct with hard walls and a base flow flowing from left to right. The duct then changes to a cylindrical thin shell which extends to the right, and is clamped to the hard-wall duct. As above, we then consider small unsteady perturbations to this steady base flow.
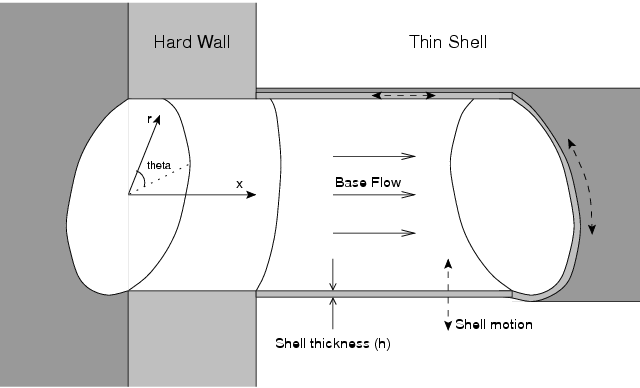
Unlike above, where the duct parameters are assumed to vary slowly along the duct, here there is a sudden change at (say) x=0. Such sudden changes may be dealt with using the Wiener–Hopf technique[3].
Figure 5 shows the results of such a Wiener–Hopf analysis for an externally damped aluminium thin shell containing air flowing at Mach number 0.5. Figure 5(a) shows a first-radial-order mode incoming from the left (maximum pressure at the top, fading gradually to zero at the bottom) scattering into a transmitted wave in the thin-shell section which dies out owing to the damping, and a reflected sixth-radial-order mode (the six horizontal bands on the left hand side). Figure 5(b) shows a closeup around the reflection point, and demonstrates that everything is smooth and well behaved there; this requires special attention during the mathematical derivation.
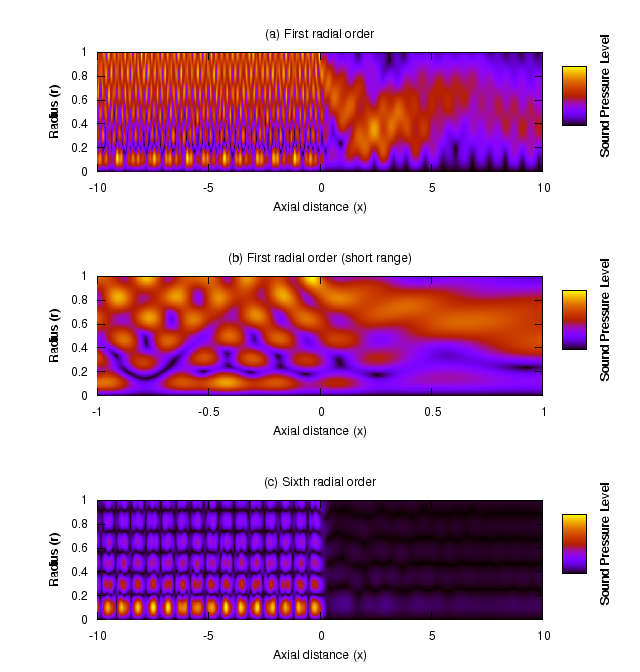
Figure 5(c) shows an incoming sixth-radial-order mode from the left, reflecting into a sixth-radial-order reflected mode on the left hand side, and virtually no transmitted mode in the thin-shell section of the duct.
While figure 5 plots the sound pressure level, it is hard to see the incoming or outgoing nature of the waves from these plots. The movies below show how the actual sound pressure in the duct varies with time. In the movies, red is a positive pressure (relative to the steady pressure) and blue is negative. The movies only show one cycle, and are best viewed looping (so that they start playing again as soon as they've finished):
- Incoming I1 mode ( 1.1MB, 1023x306)
- Incoming I6 mode ( 0.4MB, 1023x306)
References
[1] J.D. Morgan, "The interaction of sound with a subsonic cylindrical vortex layer", Proc. R. Soc. Lond. A. 344 (1975) 341–362.
[2] S.W. Rienstra, "Sound transmission in slowly varying circular and annular lined ducts with flow", J. Fluid Mech. 380 (1999) 279–296.
[3] B. Noble, Methods based on the Wiener–Hopf Technique for the Solution of Partial Differential Equations, Pergamon (1958).
