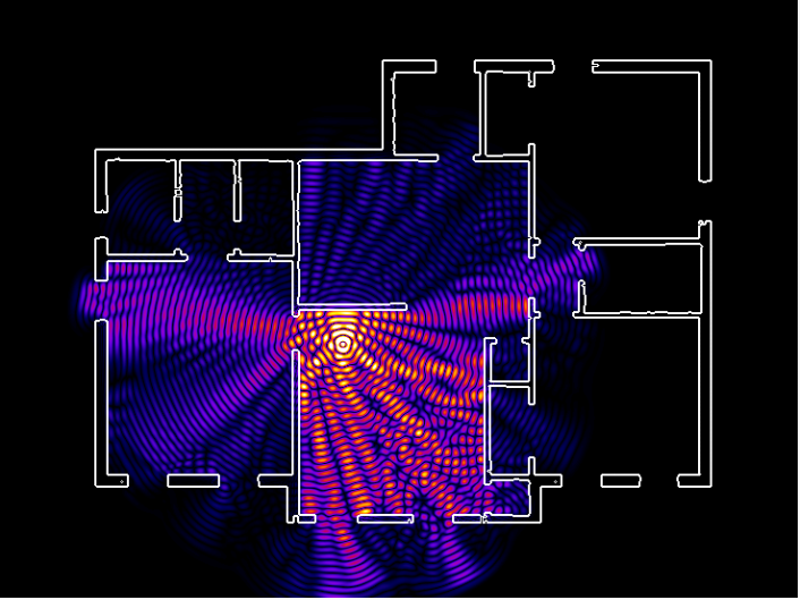
The Helmhurts app simulating wifi-coverage in a house.

Waves are all around us. Whether it is understanding wifi coverage, designing quiet vacuum cleaners, or mitigating airport noise, theoretical and computational models of waves are a useful scientific and design tool. Unfortunately, accurate computer simulations of waves are hard: they are finely balanced between being unstable and being too dissipative, and they push the bounds of what is computationally possible.

The purpose of this project is to investigate bringing together two clever theoretical ideas: wavenumber optimized implicit finite difference schemes (implicit DRP schemes); and summation by parts finite difference schemes (SBP schemes). While both were invented in the mid 1990s, and both are still the subject of current research today, they don't seem to have been combined. DRP schemes optimize finite differences to accurately simulate waves with as few points per wavelength as possible. SBP schemes are a way of treating boundaries (such as reflecting walls) that means they satisfy a property similar to integration by parts; it turns out that this means they are provably stable, while most other schemes are highly unstable near boundaries. By combining them, it should be possible to generate provably stable wave simulations needing few points per wavelength.

The project would involve a theoretical component (mostly involving matrix algebra and some optimization), and then performing a number of simulations of various test cases to investigate how well the new schemes perform. This is highly likely to lead to journal publications.

The project has very few if any pre-requisites. Knowledge of any of the following would be helpful, but is not necessary, as these could be learnt during the project:

• Simulating differential equations using finite differences.
• Linear algebra (some theory about matrices, e.g. positive definiteness).
• Simple optimization with constraints.
• Computer programming (Matlab, C++, etc).