Summary: Small random perturbations may have a dramatic impact
on the long time evolution of dynamical systems, and large deviation
theory is often the right theoretical framework to understand these
effects. At the core of the theory lies the minimization of an
action functional, which in many cases of interest has to be
computed by numerical means. Here, a numerical method is presented
to effectively compute minimizers of the Freidlin-Wentzell action
functional in very general settings. The matlab source code of the
algorithm and some test problems is available for download
here.
Introduction
Small random perturbations often have a lasting effect on the
long-time evolution of dynamical systems. For example, they give rise
to transitions between otherwise stable equilibria, a phenomenon
referred to as metastability that is observed in a wide variety of
contexts, e.g. phase separation, population dynamics, chemical
reactions, climate regimes, neuroscience, or fluid dynamics. Since the
time-scale over which these transition events occurs is typically
exponentially large in some control parameter (for example the noise
amplitude), a brute-force simulation approach to compute these events
quickly becomes infeasible. Fortunately, it is possible to exploit the
fact that the mechanism of these transitions is often predictable when
the random perturbations have small amplitude: with high probability
the transitions occur by their path of maximum likelihood (PML), and
knowledge of this PML also permits to estimate their rate. This is the
essence of large deviation theory (LDT), which applies in a wide
variety of contexts. For example, systems whose evolution is governed
by a stochastic (ordinary or partial) differential equation driven by
a small noise or by a Markov jump process in which jumps occur often
but lead to small changes of the system state, or slow/fast systems in
which the fast variables are randomly driven and the slow ones feel
these perturbations through the effect fast variables only, all fit
within the framework of LDT. Note that, typically, the dynamics of
these systems fail to exhibit microscopic reversibility (detailed
balance) and the transitions therefore occur
out-of-equilibrium. Nevertheless, LDT still applies.
LDT also indicates that the PML is computable as the minimizer of a
specific objective function (action): the large deviation rate
function of the problem at hand. This is a non-trivial numerical
optimization problem which calls for tailor-made techniques for its
solution. Here we will focus on one such technique, the geometric
minimum action method, which was designed to perform the action
minimization over both the transition path location and its
duration. This computation gives the so-called quasipotential, whose
role is key to understand the long time effect of the random
perturbations on the system, including the mechanism of transitions
events induced by these perturbations.
Simplified geometric minimum action method
Consider
$$dX = b(X) dt + \sqrt{\epsilon} \sigma(X) dW\,,$$
where \(b:
\mathbb{R}^n \to\mathbb{R}^n\) denotes the drift term, \(W\) is a
standard Wiener process in \(\mathbb{R}^n\), \(\sigma: \mathbb{R}^n \to
\mathbb{R}^n \times \mathbb{R}^n\) is related to the diffusion tensor
via \(a(x) = (\sigma \sigma^\dagger)(x)\), and \(\epsilon>0\) is a
parameter measuring the noise amplitude. Suppose that we want to
estimate the probability of an event, such as finding the solution in
a set \(B\subset \mathbb{R}^n\) at time \(T\) given that it started at
\(X(0)=x\) at time \(t=0\).
Minimization problem
In the limit as \(\epsilon\to0\), this probability can be estimated
via a minimization problem
$$\mathcal{P}^x \left(X(T)\in B\right) \asymp \exp\left(-\epsilon^{-1} \min _{\phi\in
\mathcal {C}} S_T(\phi) \right)$$
for the action functional (or rate function)
$$ S_T(\phi) =
\tfrac12\int_0^T \langle\dot \phi - b(\phi),
\left(a(\phi)\right)^{-1}(\dot \phi - b(\phi))\rangle\,dt\,.$$
Here \(\asymp\) denotes log-asymptotic equivalence (i.e. the ratio of
the logarithms of both sides tends to 1 as \(\epsilon\to0\)), the
minimum is taken over the set \(\mathcal{C} = \{ \phi\in
C([0,T],\mathbb{R}^n): \phi(0)=x,\phi(T)\in B\}\), and we assumed for
simplicity that \(a(\phi)\) is invertible and
\(\langle\cdot,\cdot\rangle\) denotes the Euclidean inner product in
\(\mathbb{R}^n\). LDT also indicates that, as \(\epsilon \to0\), when the
event occurs, it does so with \(X\) being arbitrarily close to the
minimizer \(\phi_* = \mathop{\text{argmin }} _{\phi\in \mathcal {C}}
S_T(\phi)\). We can define a Hamiltonian associated with the action
functional above via \(H(\phi,\theta) =
\langle{b(\phi)},{\theta}\rangle+\tfrac12\langle{\theta},{a(\phi)
\theta}\rangle\). Our algorithm will turn out to be valid for more than
just Hamiltonians of this form.
As detailed in Proposition 2.1 of [Heymann, Vanden-Eijnden, CPAM
61 (8), 2008], it is possible to redefine the action functional to
a geometric form,
$$\hat S(\phi) = \sup_{\theta: H(\phi,\theta=0)}
\int_0^1 \langle \phi', \theta\rangle\,ds$$
and we abbreviate \(E(\varphi,\vartheta) = \int_0^1 \langle{\varphi'},{\vartheta}\rangle\,ds\). Let
$$ E_*(\varphi) = \sup_{\vartheta:H(\varphi,\vartheta)=0} E(\varphi,\vartheta)
$$
and \(\vartheta_*(\varphi)\) such that \(E_*(\varphi) = E(\varphi,
\vartheta_*(\varphi))\). This implies that \(\vartheta_*\) fulfills the
Euler-Lagrange equation associated with
the constrained optimization problem, that is,
$$ D_\vartheta E(\varphi, \vartheta_*) = \mu H_\vartheta(\varphi,\vartheta_*)\,,$$
where on the right-hand side \(\mu(s)\) is the Lagrange
multiplier added to enforce the constraint
\(H(\varphi,\vartheta_*)=0\). In particular, at \(\vartheta=\vartheta_*\),
we have
$$ \mu = \frac{\|D_\vartheta E\|^2}{\langle\!\langle{D_\vartheta E},{H_\vartheta}\rangle\!\rangle} = \frac{\|\varphi'\|^2}{\langle\!\langle{\varphi'},{H_\vartheta}\rangle\!\rangle}\,,
$$
where the inner product \(\langle\!\langle{\cdot},{\cdot}\rangle\!\rangle\) and its induced norm
\(\|\cdot\|\) can be chosen appropriately, for example as
\(\langle{\cdot},{\cdot}\rangle\) or
\(\langle{\cdot},{H_{\vartheta\vartheta}^{-1} \,\cdot}\rangle\).
At the minimizer \(\varphi_*\), the variation of \(E_*\) with respect to \(\varphi\)
vanishes. We conclude
$$\begin{aligned}
0 = D_\varphi E_*(\varphi_*) &= D_\varphi E(\varphi_*,\vartheta_*)
+ \left[D_\vartheta E D_\varphi \vartheta
\right]_{(\varphi,\vartheta)=(\varphi_*,\vartheta_*)}\nonumber\\
&= -\vartheta_*' + \mu \left[H_\vartheta
D_\varphi \vartheta\right]_{(\varphi,\vartheta)=(\varphi_*,\vartheta_*)}
\nonumber\\
&= -\vartheta_*' - \mu
H_\varphi(\varphi_*,\vartheta_*)\,,
\label{eq:optim-psi}
\end{aligned}$$
where in the last step we used \(H(\varphi, \vartheta_*)=0\) and
therefore
$$H_\varphi(\varphi, \vartheta_*) = -
H_\vartheta(\varphi,\vartheta_*) D_\varphi \vartheta.$$
Multiplying
the gradient with any positive definite matrix as
pre-conditioner yields a descent direction. It
is necessary to choose \(\mu^{-1}\) as pre-conditioner to ensure
convergence around critical points, where \(\varphi'=0\).
Algorithm
Summarizing, we have reduced the minimization of the geometric action
into two separate tasks:
-
For a given \(\varphi\), find \(\vartheta_*(\varphi)\) by solving the
constrained optimization problem
$$\max_{\vartheta, H(\varphi,\vartheta)=0} E(\varphi,\vartheta)\,,$$
which is equivalent to solving
$$ D_\vartheta E(\varphi,\vartheta_*) = \varphi' = \mu H_\vartheta(\varphi,\vartheta_*)$$
for \((\mu,\vartheta_*)\) under the constraint \(H(\varphi,\vartheta_*)=0\). This
can be done via gradient descent, a second order algorithm for faster convergence
(e.g. Newton-Raphson) or, in many cases, analytically.
-
Find \(\varphi_*\) by solving the optimization problem
$$\min_{\varphi\in\hat{\mathcal{C}}_{x,y}} E_*(\varphi)\,,$$
for example by pre-conditioned gradient descent, using as direction
$$-\mu^{-1} D_\varphi E_* = \mu^{-1}\vartheta_*'(\varphi) + H_\varphi(\varphi,\vartheta_*(\varphi))\,,$$
with \(\mu^{-1}\) as pre-conditioner. The constraint on the
parametrization, e.g. \({|\varphi'|=\textrm{const}}\), must be fulfilled
during this descent (see below).
Applications
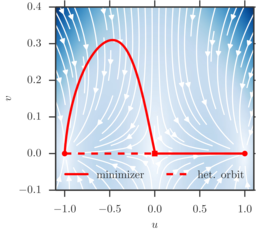
Maier-Stein model: Breaking detailed balance
Maier and Stein's model [J. Stat. Phys 83, 3–4 (1996)] is a
simple system often used as benchmark in LDT calculations. It reads
$$ \begin{cases}
du = (u-u^3-\beta u v^2) dt + \sqrt{\epsilon}dW_u\\
dv = -(1+u^2)v dt + \sqrt{\epsilon}dW_v\,,
\end{cases}$$
where \(\beta\) is a parameter. For all values of \(\beta\), the
deterministic system has the two stable fixed points,
\(\varphi_-=(-1,0)\) and \(\varphi_+=(1,0)\), and a unique unstable
critical point \(\varphi_s=(0,0)\). However it satisfies detailed
balance only for \(\beta=1\). To the right, the transition
paths between the two stable fixed points is depicted in
comparison to the heteroclinic orbit. The source code for this problem
is available below.
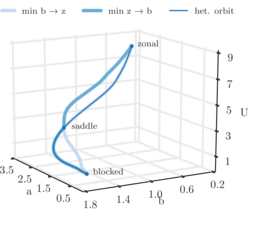
Eggers model: Meta-stable climate regimes
Egger [J. Atm. Sc. 38, 12 (1981)] introduces the following SDE system as a
crude model to describe weather regimes in central Europe:
$$\small \begin{aligned}
da =& kb(U-\beta/k^2)\,dt - \gamma a\,dt + \sqrt{\epsilon} dW_a\,,\\
db =& -ka(U-\beta/k^2)\,dt + UH/k\,dt \\&- \gamma b\,dt
+ \sqrt{\epsilon} dW_b\,,\\
dU =& -bHk/2\,dt-\gamma(U-U_0)\,dt + \sqrt{\epsilon} dW_U\,.
\end{aligned}$$
When \(\epsilon\) is small, these equation exhibit metastability between
a "blocked state" and a "zonal state". To the right, the transition
paths between these two states is depicted in comparison to the
heteroclinic orbit. The source code for this problem is available
below.
Allen-Cahn/Cahn-Hilliard model: Phase separation and growth
Consider the SDE system
$$ d\phi= (\frac1\alpha Q (\phi-\phi^3) -
\phi)dt + \sqrt{\epsilon} dW$$
with \(\phi=(\phi_1, \phi_2)\) and the
matrix \(Q=((1,-1),(-1,1))\). This system does not satisfy detailed
balance, as its drift is made of two gradient terms with incompatible
mobility operators (namely \(Q\) and \(\textrm{Id}\)). This model can be
seen as a 2-dimensional reduction to a discretized version of the
continuous Allen-Cahn/Cahn-Hilliard. When \(\alpha\) is small, there
exists a "slow manifold", comprised of all points where
\(Q(\phi-\phi^3)=0\) which is shown as a white dashed line to the
right. On this manifold, the deterministic dynamics are of order
\(O(1)\), which is small in comparison to the dynamics of the \(Q\)-term,
which are of order \(O(1/\alpha)\). This suggests that for small enough
\(\alpha\) the transition trajectory will follow this slow manifold on
which the drift is small, rather than the heteroclinic orbit, to
escape the basin of the stable fixed points. This intuition is
confirmed in the plot to the right. The source code for this problem
is available below.
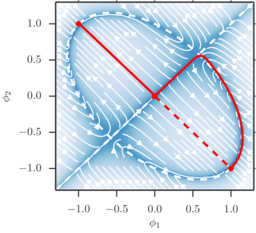
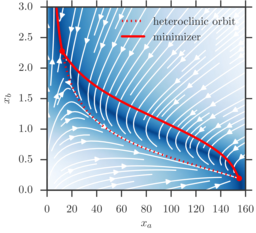
Genetic switch: A non-quadratic Hamiltonian
The algorithm can readily be applied to situations, where the
Hamiltonian is non-quadratic. This is the case for example for
birth-death-processes with a positive feedback loop, modeled as
continuous time Markov process. The model
$$
\begin{aligned}H(\phi,\theta) &=
\frac{a_1}{1+\phi_b^3}(e^{\theta_a}-1) + \phi_a(e^{-\theta_a}-1)\\&+
\frac{a_2}{1+\phi_a}(e^{\theta_b}-1) +
\phi_b(e^{-\theta_b}-1)\end{aligned}$$
with \(a_1=156, a_2=30\) was
first defined by Roma et al. [Phys. Rev. E 71 (2005)] to model a genetic
switching mechanism in molecular dynamics. The deterministic dynamics
for this model follow along with minimizer and heteroclinic orbit for
this setup are depicted to the right (zoomed into the "uphill"
region).
Source code
Matlab source code with the generic algorithm and most of the examples
above is available here
Relevant publications
-
T. Grafke, and E. Vanden-Eijnden,
"Numerical computation of rare events via large deviation theory",
Chaos 29 (2019), 063118 (link)
-
T. Grafke, T. Schäfer, and E. Vanden-Eijnden, "Long Term Effects
of Small Random Perturbations on Dynamical Systems: Theoretical and
Computational
Tools",
Fields Institute Communications, In: Recent Progress and Modern
Challenges in Applied Mathematics, Modeling and Computational
Science (Springer, New York, NY) (2017)
(link)
-
T. Grafke, and E. Vanden-Eijnden, "Non-equilibrium transitions in
multiscale systems with a bifurcating slow
manifold"
J. Stat. Mech 2017/9 (2017) 093208
(link)
-
T. Grafke, M. Cates, and E. Vanden-Eijnden, "Spatiotemporal
Self-Organization of Fluctuating Bacterial
Colonies",
Phys. Rev. Lett. 119 (2017), 188003
(link)