|
We now utilise the approach given in
programs 6.3 and 6.4 to implement event-driven stochasticity into the
standard
SIR equations when there is the potential for stochastic imports of
infection. Although disease incidence in real populations may
frequently undergo stochastically driven fade-outs, imports of pathogen
from outside the population can prevent permanent extinction. In human
populations, such imports usually take the form of visitors who remain
for a limited period but, in doing so, re-introduce the pathogen. Here
we model imports in two distinct ways:
1) Imports due to an external force of infection, which occur at rate
εX,
2) Imports due to an infected individual moving into the population,
which occur at rate δ.
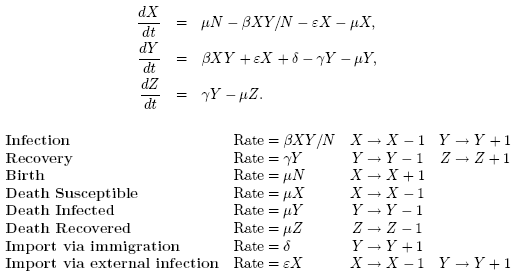
Once again we assume that the
population size N is constant
which prevents the permanent extinction of the host population.
Note that we are using numbers
(X,Y,Z) throughout this chapter for greater clarity.
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| μ |
is
the per capita death
rate.
|
| ε |
is
the import rate due to an external force of infection
|
| δ |
is
the import rate due to infectious individuals immigrating into the
population
|
| X(0) |
is
the initial number or density of susceptible individuals. |
| Y(0) |
is
the initial number or density of infectious individuals. |
N
|
is
the population
size -- assumed to be constant. We assume Z(0)=N-X(0)-Y(0)
|
All
rates are
specified
in days.
Requirements.
All parameters must be positive. Remember, X, Y, Z and N all refer to integer
numbers.
Files
Python Program, MATLAB Code.
|


