|
An intuitive way to incorporate noise
is to introduce it directly into the deterministic equations. As such,
the dynamics at each point in time are subject to some random
variability and this variability is propagated forward in time by the
underlying equations. We are, therefore, concerned with the interplay
between deterministic and stochastic forces—how they cancel out or
amplify each other.
As a starting point, let us incorporate noise into only the
transmission term. Let ξ(t) be a time series of random deviates
derived from the normal distribution with mean zero and unit variance
(see Box 6.2). The basic equations, assuming frequency-dependent
(mass-action) transmission, are transformed to:
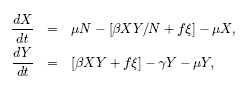
Note that we are using numbers
(X,Y,Z) throughout this chapter for greater clarity.
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
f
|
amount
of noise experienced in the transmission term.
|
ξ
|
noise
term which is generated as a function of the time step.
|
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| μ |
is
the per capita birth and death
rate.
|
| X(0) |
is
the initial number or density of susceptible individuals. |
| Y(0) |
is
the initial number or density of infectious individuals. |
N
|
is
the population
size -- assumed to be constant.
|
All rates are
specified
in days.
Requirements.
All parameters must be positive. Remember, X, Y and N all refer to numbers.
A time step δt also has to be defined and this sets both the
integration step and scales the noise term ξ.
Files
Python Program, MATLAB Code.
|


