|
The overwhelming drawback associated
with using the Direct Method of Gillespie is their slow simulation
times for large population sizes. Gillespie (2001) has recently
proposed minor sacrifices in simulation accuracy in order to obtain
substantial gains in simulation speed. The new algorithm is called the
“τ -leap method” and may be explained as follows:
1) A time step tau is choosen and is assumed to be fixed throughout the
simulation
2) Each time step, the number of times an event occurs is assumed to be
Poisson distributed with a mean given by the rates of change.
3) The events are performed, the population variables and the time
updated and the process is repeated.
For the SIR model this translates to the following:
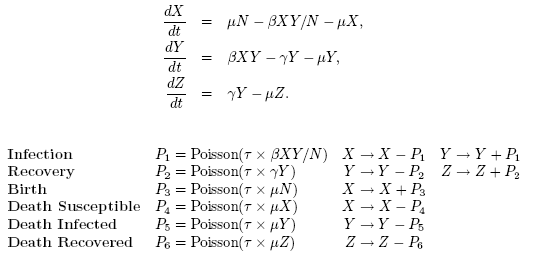
The approximation comes from assuming
that the multiple events that occur during a time-step are independent
and do not effect the rates of change. This approximation is most
accurate when few events occur in each time-step, but the method is
fastest when many events occurs each step -- striking the correct
balance needs care.
Note that we are using numbers
(X,Y,Z) throughout this chapter for greater clarity.
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| μ |
is
the per capita death
rate.
|
| τ |
is the time-step that is taken
each time, which can potentially contain multiple Poisson distributed
events.
|
| X(0) |
is
the initial number or density of susceptible individuals. |
| Y(0) |
is
the initial number or density of infectious individuals. |
N
|
is
the population
size -- assumed to be constant. We assume Z(0)=N-X(0)-Y(0)
|
All
rates are
specified
in days.
Requirements.
All parameters must be positive. Remember, X, Y, Z and N all refer to integer
numbers.
In addition we need to specify a time-step τ.
Files
Python Program, MATLAB Code.
|


