Research interests
Kinetic models for opinion formation
The formation of opinions in a society has been a frequent research subject due to its important applications as election processes or referendums. Often, especially in numerical simulation studies, cellular automata are used. Another approach uses models of mean field type, which lead to systems of (ordinary or partial) differential equations. A third approach is to study kinetic models of opinion formation. Exchange of opinion between individuals in these models is defined by pairwise, microscopic interactions. In dependence on the specification of these interactions, the whole society develops a certain macroscopic opinion distribution. The literature primarily has focused on election processes, referendums or public opinion tendencies. Less attention has been paid to the important effect that opinion leaders have on the dissemination of new ideas and the diffusion of beliefs in a society.
state elections in Carinthia, Austria
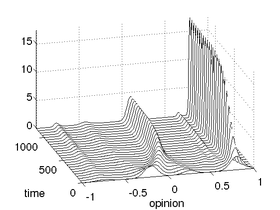
In [1] we propose a mathematical model for opinion formation in a society which is built of two groups, one group of `ordinary' people and one group of `strong opinion leaders'. Our approach is based on an opinion formation model introduced in [2] and borrows ideas from the kinetic theory of mixtures of rarefied gases. Starting from microscopic interactions among individuals, we arrive at a macroscopic description of the opinion formation process which is characterized by a system of Fokker-Planck type equations. We discuss the steady states of this system, extend it to incorporate emergence and decline of opinion leaders, and present numerical results. As an example, we use our model to simulate the 2009 state elections in Carinthia, Austria, see also the SIAM News article [3].
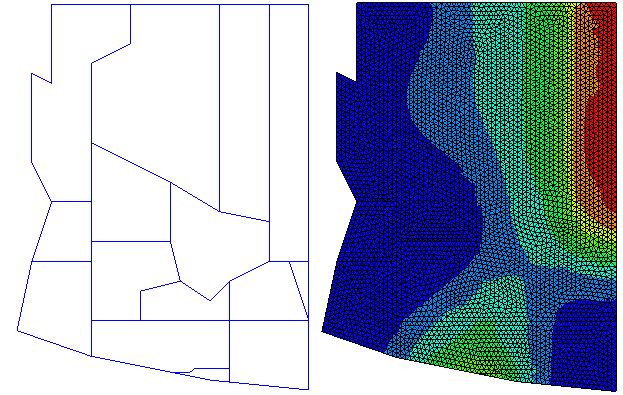
numerical solution of the Fokker-Planck type equation
In [4] we propose and investigate different kinetic models for opinion formation, when the opinion formation process depends on an additional independent variable, e.g. a leadership or a spatial variable. More specifically, we consider
- opinion dynamics under the effect of opinion leadership, where each individual is characterized not only by its opinion but also by another independent variable which quantifies leadership qualities;
- opinion dynamics modelling political segregation in ‘The Big Sort’, a phenomenon that US citizens increasingly prefer to live in neighbourhoods with politically like-minded individuals.
References
[1] B. Düring, P.A. Markowich, J.-F. Pietschmann, and M.-T. Wolfram. Boltzmann and Fokker-Planck equations modelling opinion formation in the presence of strong leaders. Proc. R. Soc. Lond. A 465(2112), 3687-3708, 2009. (preprint)[2] G. Toscani. Kinetic models of opinion formation, Commun. Math. Sci. 4(3) 481-496, 2006.
[3] B. Düring. Kinetic modelling of opinion leadership. SIAM News 44(10), December 2011, pp. 1, 8.
[4] B. Düring and M.-T. Wolfram. Opinion dynamics: inhomogeneous Boltzmann-type equations modelling opinion leadership and political segregation. Proc. R. Soc. Lond. A 471 (2015), 20150345. (arXiv:1505.07433)
[5] B. Düring. Partial differential equations model political segregation. SIAM News Blog, 8 June 2017.
Structure-preserving variational discretisations of nonlinear partial differential equations with a Wasserstein gradient flow structure
Evolution equations with an underlying gradient flow structure have since long been of special interest in analysis and mathematical physics. In particular, transport equations that allow for a variational formulation with respect to the L2-Wasserstein metric have attracted a lot of attention recently. The gradient flow formulation gives rise to a natural semi-discretization in time of the evolution by means of the minimizing movement scheme (see, e.g. [1]), which constitutes a time-discrete minimization problem for the (sum of kinetic and potential) energy. On the other hand, nonlinear diffusion equations of fourth (and higher) order have become increasingly important in pure and applied mathematics. Many of them could be formulated in a variational framework as well, i.e., they have been interpreted as gradient flows with respect to some metric structure. Well-known examples are Cahn-Hilliard equations modeling gas mixtures, lubrication equations describing the rupture of thin viscous films, and fluid-type quantum models for semiconductors device simulations.
using the Wasserstein gradient flow scheme
When it comes to solve equations of a gradient flow type numerically, it is natural to ask for appropriate schemes that respect the equation's special structure in some way. In [3], we propose and study a fully discrete variant of the minimizing movement scheme for numerical solution of the nonlinear fourth order Derrida-Lebowitz-Speer-Spohn equation (cf. [2]). Our method is iterative and consists of an outer and an inner loop. In each time step of the outer loop a constrained quadratic optimization problem for the Fisher information is solved on a finite-dimensional space of ansatz functions. These subproblems are solved iteratively in the inner loop by applying Newton's method to the optimality system, leading to a sequential quadratic programming method. In result, we obtain a fully practical numerical scheme for a non-linear fourth order equation that respects its Wasserstein gradient flow structure. By construction it dissipates the Fisher information in the fastest way possible, just like the original gradient flow. Other benefits are built-in conservation of mass and non-negativity of the solution. Its formulation in Lagrangian coordinates induces a time-dependent spatial grid that is naturally adaptive to the movement of the density. Moreover, since our method derives from the implicit minimizing movement scheme, it does not suffer from restrictions on the time step size. Indeed, the numerical results suggest unconditional stability of the scheme. Although our presentation is focused on the DLSS equation, the proposed numerical method easily adapts to a wide class of Wasserstein gradient flows, replacing the Fisher information by other potentials.
using the Lagrangian gradient flow scheme
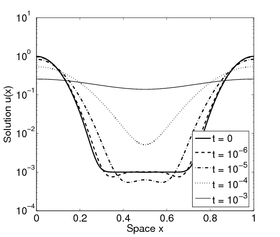
A Lagragian numerical scheme for solving nonlinear degenerate Fokker-Planck equations in multiple space dimensions is developed in [4]. It applies to a large class of nonlinear diffusion equations, whose dynamics are driven by internal energies and given external potentials, e.g. the porous medium equation and the fast diffusion equation. The key ingredient in our approach is again the gradient flow structure of the dynamics. For discretization of the Lagrangian map, we use a finite subspace of linear maps in space and a variational form of the implicit Euler method in time. Thanks to that time discretisation, the fully discrete solution inherits energy estimates from the original gradient flow, and these lead to weak compactness of the trajectories in the continuous limit. A variety of numerical experiments for the porous medium equation indicates that the scheme is well-adapted to track the growth of the solution's support.
References
[1] L. Ambrosio and G. Savaré. Gradient flows of probability measures. In: Handbook of Evolution Equations, Dafermos, C. and Feireisl, E. (eds.), Vol. 3, pp. 1-136, Elsevier, 2006.[2] A. Jüngel and D. Matthes. The Derrida-Lebowitz-Speer-Spohn equation: existence, nonuniqueness, and decay rates of the solutions. SIAM J. Math. Anal. 39(6), 1996-2015, 2008.
[3] B. Düring, D. Matthes, and J.-P. Milisic. A gradient flow scheme for nonlinear fourth order equations. Discrete Contin. Dyn. Syst. Ser. B 14(3) (2010), 935-959. (preprint)
[4] J.A. Carrillo, B. Düring, D. Matthes and D.S. McCormick. A Lagrangian scheme for the solution of nonlinear diffusion equations using moving simplex meshes. J. Sci. Comput. 75(3) (2018), 1463-1499. (arXiv:1702.01707)
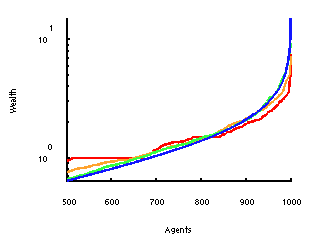
Kinetic models for optimal control of wealth inequalities
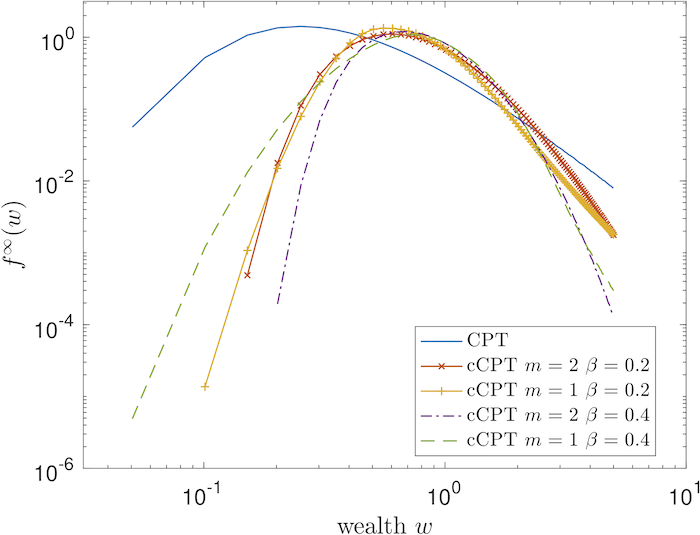
In [1] we discuss optimal control strategies for kinetic models for wealth distribution in a simple market economy, with the aim to reduce the wealth inequality in the population. Usual government policies employ proportional taxation, with the expectation that a progressive tax system would prevent excess concentration of wealth.Our analysis is based on a finite time horizon approximation, or model predictive control, of the corresponding control problem for the microscopic agents' dynamic and results in an alternative theoretical approach to the taxation and redistribution policy at a global level. It is shown that in general the control is able to modify the Pareto index of the stationary solution of the corresponding Boltzmann kinetic equation, and that this modification can be exactly quantified. Connections between previous Fokker-Planck based models and taxation-redistribution policies and the present approach are also discussed.
References
[1] B. Düring, L. Pareschi and G. Toscani. Kinetic models for optimal control of wealth inequalities. Eur. Phys. J. B 91(10) (2018), 265. (arXiv:1803.02171)High-order compact finite differences for parabolic problems
In [1] we derive a new high-order compact finite difference scheme for option pricing in stochastic volatility models. The scheme is fourth order accurate in space and second order accurate in time. Under some restrictions, theoretical results like unconditional stability in the sense of von Neumann are presented. Numerical experiments for the European option pricing problem are presented which show fourth order convergence for non-smooth payoff. A further discussion of the scheme's stability is performed in [2].
In [3] we extend the high-order compact finite difference approach for option pricing in stochastic volatility models to non-uniform grids. In our numerical study we obtain high-order numerical convergence also for non-zero correlation and non-smooth payoffs which are typical in option pricing. In all numerical experiments a comparative standard second-order discretisation is significantly outperformed. We conduct a numerical stability study which indicates unconditional stability of the scheme.
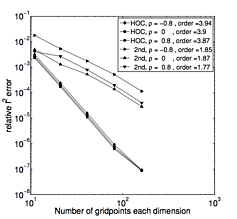
In [4] we consider a rather general class of parabolic partial differential equations with time and space dependent coefficients as well as with mixed second-order derivative terms in n spatial dimensions. Problems of this type arise frequently in computational fluid dynamics and computational finance. We follow a high-order compact finite difference approach and derive general conditions on the coefficients which allow us to obtain a high-order compact scheme which is fourth-order accurate in space and second-order accurate in time. Moreover, we perform a thorough von Neumann stability analysis of the Cauchy problem in two and three spatial dimensions for vanishing mixed derivative terms, and also give partial results for the general case. The results suggest unconditional stability of the scheme. As an application example we consider the pricing of European Power Put Options in the multidimensional Black-Scholes model for two and three underlying assets.
References
[1] B. Düring and M. Fournié. High-order compact finite difference scheme for option pricing in stochastic volatility models. J. Comput. Appl. Math. 236(17) (2012), 4462-4473. (arXiv:1404.5140) (SSRN:1646885)[2] B. Düring and M. Fournié. On the stability of a compact finite difference scheme for option pricing. In: Progress in Industrial Mathematics at ECMI 2010, M. Günther et al. (eds.), pp. 215-221, Springer, Berlin, Heidelberg, 2012. (preprint)
[3] B. Düring, M. Fournié, and C. Heuer. High-order compact finite difference schemes for option pricing in stochastic volatility models on non-uniform grids. J. Comput. Appl. Math. 271 (2014), 247-266. (arXiv:1404.5138) (SSRN:2295581)
[4] B. Düring and C. Heuer. High-order compact schemes for parabolic problems with mixed derivatives in multiple space dimensions. SIAM J. Numer. Anal. 53(5) (2015), 2113-2134. (arXiv:1506.06711) (SSRN:2459861)
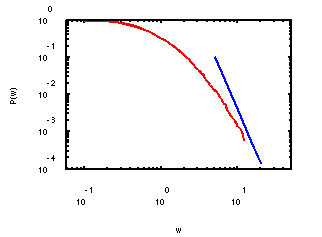
Kinetic models for wealth distribution
According to empirical data, the wealth distribution (denoting the density of agents with wealth w>0) among the population in western countries shows a Pareto tail w-ν, named after the economist Vilfredo Pareto. A postulate in the field of econophysics is that the laws of statistical mechanics for particle systems can also be used to model the trade interactions between agents in a simple market. Just as a classical kinetic model is defined by prescribing the collision kernel for the microscopic particle interactions, the econophysical model is defined by prescribing the exchange rules for wealth in trades. In dependence on these microscopic rules, the system develops macroscopic features in the long-time limit as the Pareto tail of the wealth distribution.
In [3,4] we compare different types of econophysical models which are able to produce Pareto tails, in particular the Cordier-Pareschi-Toscani (CPT) and the Chakrabarti-Chatterjee-Manna (CCM) model. The CPT model has been introduced in [1], and was intensively studied only recently [2]. When two agents with pre-trade wealths interact, they exchange part of their wealth while while retaining a certain fraction of it. This fraction is quantified by the saving propensity. Risky investments are modelled by random variables with mean zero. Thus, the CPT model preserves the total wealth in the statistical mean. In [3] it is proved that any solution f(t) converges to the steady state exponentially fast in suitable Fourier and Wasserstein metrics, while the Wasserstein distance in the CCM model can at best decay algebraically in time. Numerical simulations confirm the theoretical results.
In [5] we introduce and discuss the passage to hydrodynamic equations for kinetic models of conservative economies, in which the density of wealth depends on additional parameters, like the propensity to invest. As in kinetic theory of rarefied gases, the closure depends on the knowledge of the homogeneous steady wealth distribution (the Maxwellian) of the underlying kinetic model. Numerical simulations on the fluid equations are proposed and analyzed for various laws of variation of the propensity.
An extension of the CPT model to an economy which is built of a number of countries or social groups is developed in [6]. Wealth is exchanged by individuals inside these countries (domestic trade) as well as in between different countries (international trade). Under a suitable scaling we derive a system of Fokker-Planck type equations and discuss its extension to a two-dimensional model with distributed trading propensity. Theoretical and numerical results for two groups show that the wealth distribution develops a bimodal (and in general, a polymodal) shape.
References
[1] S. Cordier, L. Pareschi, and G. Toscani. On a kinetic model for a simple market economy. J. Stat. Phys. 120 (2005), 253-277.[2] D. Matthes and G. Toscani. On steady distributions of kinetic models of conservative economies. J. Stat. Phys. 130(6) (2008), 1087-1117.
[3] B. Düring, D. Matthes, and G. Toscani. Exponential and algebraic relaxation in kinetic models for wealth distribution. In: "WASCOM 2007" - Proceedings of the 14th Conference on Waves and Stability in Continuous Media, N. Manganaro et al. (eds.), pp. 228-238, World Sci. Publ., Hackensack, NJ, 2008. (preprint)
[4] B. Düring, D. Matthes, and G. Toscani. Kinetic equations modelling wealth redistribution: a comparison of approaches. Phys. Rev. E 78(5) (2008), 056103. (preprint)
[5] B. Düring and G. Toscani. Hydrodynamics from kinetic models of conservative economies. Physica A 384(2) (2007), 493-506. (preprint)
[6] B. Düring and G. Toscani. International and domestic trading and wealth distribution. Comm. Math. Sci. 6(4) (2008), 1043-1058. (preprint)
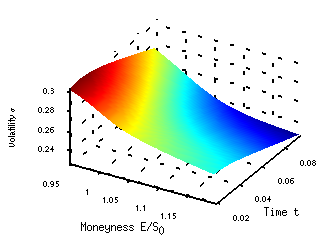
Optimal control: Volatility estimation from market option prices
Several approaches for solving the calibration problem of computing local volatility functions from market data in a generalized Black-Scholes setting have been discussed in the literature. Most of them focus on the numerical results obtained by standard methods without analyzing in-depth the algorithms used. In [2], we follow an optimal control approach [1] in a Lagrangian framework to solve the problem. We show the existence of a global solution and study first- and second-order optimality conditions. We propose an algorithm, that is based on a globalized sequential quadratic programming (SQP) method with a modified Hessian as an outer loop. In each iteration a linear-quadratic optimal control problem with box constraints is solved by a primal-dual active set strategy in an inner loop.
Alternatively, one can modify the approach and not iterate until convergence in the inner loop. Only one step of the primal-dual active set method is then performed in each SQP iteration. This leads to a semi-smooth Newton method [3], that converges locally superlinearly. The relationship between the primal dual active set strategy and semi-smooth Newton methods has been investigated in [4].
References
[1] R. Lagnado and S. Osher. A technique for calibrating derivative security pricing models: numerical solution of an inverse problem. J. Comput. Finance 1 (1997), 13-25.[2] B. Düring, A. Jüngel, and S. Volkwein. Sequential quadratic programming method for volatility estimation in option pricing. J. Optim. Theory Appl. 139(3) (2008), 515-540. (preprint)
[3] B. Düring. A semi-smooth Newton method for an inverse problem in option pricing. Proc. Appl. Math. Mech. 7(1) (2007), Special Issue: Sixth International Congress on Industrial Applied Mathematics (ICIAM07) and GAMM Annual Meeting, Zürich 2007, 1081105-1081106. (preprint)
[4] M. Hintermüller, K. Ito, and K. Kunisch. The primal-dual active set strategy as a semi-smooth Newton method. SIAM J. Optim. 13 (2003), 865-888.
[5] B. Düring. Calibration problems in option pricing. In: Nonlinear Models in Mathematical Finance: New Research Trends in Option Pricing, M. Ehrhardt (ed.), pp. 323-352, Nova Sci. Publ., Inc., Hauppauge, NY, 2008.
Asset and option pricing with generalized pricing kernels
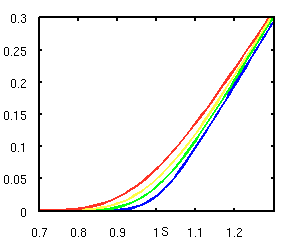
Option prices are higher for pricing kernels
with declining elasticity than for the constant
elasticity (Black-Scholes) ASPK.
Asset pricing for stocks, bonds, or derivatives is based on expectations about future cash flows and risk preferences. This view is emphasized by an equilibrium approach, the stochastic discount factor or pricing kernel approach, which goes back to Rubinstein [1] and Brennan [2]. Another, traditional approach is to specify an asset price process exogenously and price by no-arbitrage arguments. The seminal example of this approach is Black and Scholes paper [3] on pricing of European-style options. Bick [4] reconciles both approaches by showing that the geometric Brownian motion is consistent with a representative investor economy and that given the representative investor maximizes a von Neumann-Morgenstern utility function over terminal wealth and the asset represents total wealth, such a stochastic process implies constant relative risk aversion.
In [6] and [7], we follow the pricing kernel approach. The pricing kernel has the property that the forward asset price equals the expected value of the product of the terminal asset value and the pricing kernel. Mathematically, the pricing kernel characterizes the change from the subjective probability measure to the risk-neutral (or equivalent martingale) measure. In this view, any pricing problem is completely determined by the distribution of terminal asset value and the shape of the asset specific pricing kernel (ASPK). The asset specific pricing kernel is the pricing kernel conditioned on the payoffs of an asset. For a detailed discussion of the pricing kernel and the asset specific pricing kernel we refer to [5].
Rubinstein [1] and Brennan [2] make explicit assumptions on the distribution and the ASPK. More precisely, they assume a representative investor and thus the representative investor's utility function characterizes the ASPK. Similar, Black and Scholes [3] assume that the underlying is lognormally distributed, i.e., the information process follows a geometric Brownian motion, and investors are constant relative risk averse, or the asset specific pricing kernel has constant elasticity with respect to the underlying asset (cf. [4]). These assumptions lead to simple, explicit pricing formulas. However, empirical research revealed that they are not able to explain important effects in real financial markets, e.g. the volatility smile (or skew) in option prices, serial correlation in asset returns and excess and random volatility.

time-dependent ASPK. It shows crash-like patterns,
which are endogeneously explained by rational
investor behavior.
In [6], we analyze the impact of non-constant elasticity of the ASPK on option prices. Our option pricing formulas are based on a class of generalized ASPKs with declining elasticity. This relates to declining relative risk aversion for the representative investor or to the aggregation of a number of heterogeneous investors. This specification of the pricing kernel is found to be rather flexible so that many different characteristics of real markets can be matched. We validate it by successfully fitting it to empirical market data implied by S&P 500 option prices. We also compare it to other approaches to model the ASPK used in previous empirical studies. We derive explicit, analytical option pricing formulas, when the underlying information process is characterized by a lognormal, log-gamma, normal or uniform distribution, with a single risk factor. Special cases that are included in our results are generalizations of the Black and Scholes (1973) option pricing formula and the Heston (1993) option pricing formula for non-constant elasticity of the ASPK. We show that declining relative risk aversion leads to serial correlation in asset returns and smile effects in option implied volatility.
In real financial markets, not only asset returns are subject to risk, but also the estimate of the riskiness is typically subject to significant uncertainty. To incorporate such additional source of randomness into an asset pricing model, one has to introduce a second risk factor. Based on the general specification of the asset specific pricing kernel, we develop a pricing model using an information process driven by a two-dimensional diffusion with stochastic volatility in [7]. We derive analytical asset and option pricing formulas. Our model provides an explanation for crash-like phenomena in time series of asset prices based on a rational expectations approach. It also seems to be a promising approach for pricing options on a stock index as the S&P 500, since it allows to fit reasonable levels of kurtosis and skewness while using model parameters from time-series data. Credit spreads computed from our model in a simple structural model framework show quantitatively and qualitatively nice features. Moreover, our approach provides a convenient and more precise way to analyze the quantitative implications of non-constant elasticity of the ASPK.
References
[1] M. Rubinstein. The Valuation of Uncertain Income Streams and the Pricing of Options, Bell J. Econ. Manag. Sci. 7 (1976), 407-425.[2] M.J. Brennan. The Pricing of Contingent Claims in Discrete Time Models, J. Finance 34 (1979), 53-68.
[3] F. Black, M. Scholes. The Pricing of Options and Corporate Liabilities, J. Polit. Econ. 81 (1973), 637-654.
[4] A. Bick. On the Consistency of the Black-Scholes Model with a General Equilibrium Framework, J. Financial Quant. Anal. 22 (1987), 259-275.
[5] J.H. Cochrane. Asset Pricing, Princeton University Press, 2001.
[6] B. Düring and E. Lüders. Option prices under generalized pricing kernels. Rev. Deriv. Res. 8(2) (2005), 97-123. (preprint)
[7] B. Düring. Asset pricing under information with stochastic volatility. Rev. Deriv. Res. 12(2) (2009), 141-167. (preprint)
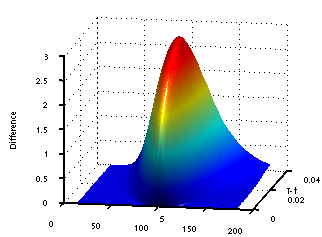
High-order compact finite differences for fully nonlinear Black-Scholes equations
In the mathematical literature, there are many papers on numerical methods for option pricing, mostly addressing the one-dimensional case and using standard, second order finite difference methods. More recently, high-order finite difference schemes (fourth order in space) were proposed that use a compact stencil, i.e. three points in space in one or nine points in space in two space dimensions.
In [2] a fully nonlinear Black-Scholes equation which models transaction costs [1] is discretized by a new high order compact scheme. Models as in [1] have been proposed to weaken one or more of the unrealistic assumptions that are made in the derivation of the classical Black-Scholes equation. These models frequently result in strongly or fully nonlinear, possibly degenerate, parabolic diffusion-convection equations for the option price. The new compact scheme is proved to be unconditionally stable and non-oscillatory and is generally more efficient than the considered classical schemes. Moreover, it is shown in [3] that the finite difference solution converges locally uniformly to the unique viscosity solution of the continuous equation. The convergence proof is based on a careful study of the discretization matrices and on an abstract convergence result of Barles and Souganides.
References
[1] G. Barles and H.M. Soner. Option Pricing with transaction costs and a nonlinear Black-Scholes equation. Finance Stochast. 2 (1998), 369-397.[2] B. Düring, M. Fournié, and A. Jüngel. High-order compact finite difference schemes for a nonlinear Black-Scholes equation. Intern. J. Theor. Appl. Finance 6(7) (2003), 767-789. (preprint)
[3] B. Düring, M. Fournié, and A. Jüngel. Convergence of a high-order compact finite difference scheme for a nonlinear Black-Scholes equation. Math. Mod. Num. Anal. 38(2) (2004), 359-369. (preprint)
Existence and uniqueness of solutions to a quasilinear parabolic equation with quadratic gradients
A quasilinear parabolic equation with quadratic gradient terms is analyzed. The equation models an optimal portfolio in so-called incomplete financial markets consisting of risky assets and non-tradable state variables. Its solution allows to compute an optimal portfolio strategy. The existence of weak global-in-time solutions in any dimension is shown under natural hypotheses. The proof is based on the monotonicity method of Frehse. Furthermore, the uniqueness of solutions is shown under a smallness condition on the derivatives of the covariance matrices using a nonlinear test function technique developed by Barles and Murat. The influence of the non-tradable state variables on the optimal value function is illustrated by a numerical example in three dimensions.