
|
In order to examine the relative
dynamical consequences of different forms of seasonality, we now focus
on wildlife diseases more closely and explore model dynamics using
parameters estimated for Rabbit Hemorrhagic Disease in the United
Kingdom. In contrast to the above examples of seasonal variation in
wildlife populations, we now allow both
the transmission rate and the per capita birth rate to be seasonally
varying. In addition, following the generally observed behavior of
natural populations, we include :
- density-dependent regulation of the hosts (in terms of an
increased death rate),
- mortality due to infection
- density-dependent transmission of infection.
These necessitates us to construct the differential equations in terms
of numbers of susceptible and infected hosts, as well as keeping track
of the total population size:
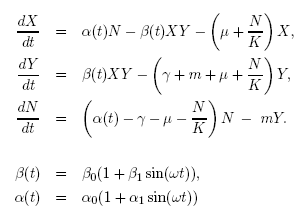
We note that for the default
parameters, Rabbit Hemorrhagic Disease has a devastating impact on the
host population density.
| β0 |
is
the mean transmission
rate |
| β1 |
is
the amplitude of sinuoidal forcing
|
| α0 |
is
the mean birth
rate |
| α1 |
is
the amplitude of sinuoidal forcing for the birth rate |
ω
|
is
the frequency of the oscillations. We set ω=2π/365, such that
oscillations are annual.
|
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| μ |
is
the per capita death
rate, and the population level birth rate. |
m
|
is the mortality rate due to
infection (note, for the default parameters mortality is very high)
|
K
|
is
the carrying capacity associated with the host populations
|
| X(0) |
is
the initial number of susceptible hosts (rabbits). |
| Y(0) |
is
the initial number infectious hosts (rabbits). |
N(0)
|
is the intital total population
size.
|
All rates are
specified
in days.
Requirements.
All parameters must be positive, α1, β1
≤ 1, and X(0)+Y(0) ≤ N(0)
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|
|


