|
A large number of species experience
seasonal forcing, either due to host aggregating a certain times of the
year, or due to transmission rates being influenced by climatic
conditions. We begin to analyse such seasonally forced systems,
by making the transmission rate β
vary sinusoidally about its mean value. This system of equations was
first studied by Klaus Dietz in 1976, when he showed the complex
dynamics that could arise from including a small amount of sinusoidal
forcing. The basic equations are as follows:
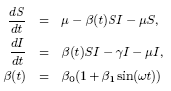
It should be noted that large values
of β1 can lead to
large-amplitude fluctuations and numerical errors.
| β0 |
is
the mean transmission
rate |
| β1 |
is
the amplitude of sinuoidal forcing
|
ω
|
is
the frequency of the oscillations. We set ω=2π/365, such that
oscillations are annual.
|
| μ |
is
the per capita death
rate, and the population level birth rate.
|
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| S(0) |
is
the initial
proportion of the population that are susceptible. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
The programs can return either standard time-series, or bifurcation
plots. Bifurcation plots are achieved by setting β1 to be a vector in the
Matlab code, or by setting Num_Bif_Steps in the parameter file for the
C and Fortran code.
Requirements.
All parameters must be positive, β1
≤ 1, and S(0)+I(0) ≤ 1
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|


