|
An alternative model of
seasonal forcing, based very much on the behaviour of measles and other
childhood-diseases, is to include term-time forcing. As such the
transmission rate is higher during school terms and lower during school
holidays. The equations become:
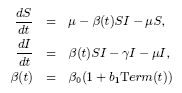
Where Term is +1 during the school
terms and -1 during the holidays.
| β0 |
is
the mean transmission
rate |
| b1 |
is
the amplitude of term-time forcing
|
| μ |
is
the per capita death
rate, and the population level birth rate.
|
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| S(0) |
is
the initial
proportion of the population that are susceptible. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
The programs can return either standard time-series, or bifurcation
plots. Bifurcation plots are achieved by setting b1 to be a vector in the
Matlab code, or by setting Num_Bif_Steps in the parameter file for the
C and Fortran code.
Requirements.
All parameters must be positive, b1
≤ 1, and S(0)+I(0) ≤ 1
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|


