|
Numerous infectious
diseases
confer no long-lasting immunity, such as rotaviruses, sexually
transmitted infections, and many bacterial infections. For these
diseases, a individuals can be infected multiple times throughout their
lives, with no apparent immunity. Here, we concentrate briefly on this
class of models, called SIS
because recovery from infection is followed by an instant return to the
susceptible pool.
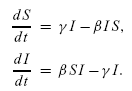
By far the most common
use of
the SIS model is to
capture the dynamics of sexually transmitted infections. Even without
births, this set of equations has an endemic equilibrium as recoverying
individuals replenish the pool of susceptibles.
We note that S+I =1, so in practise the S equation is redundant.
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
Requirements.
All parameters must be positive, and I(0)
≤ 1. Note that S=1-I
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|