|
If we are interested in
exploring the longer-term persistence and
endemic dynamics of an infectious disease, then clearly demographic
processes will be important. The simplest and most common way of
introducing demography into the SIR model is to assume there is a
natural host “lifespan”, 1/μ
years. Then, the rate at which individuals (in any epidemiological
class) suffer natural mortality is given by μ. It is important to emphasize
that this factor is independent of the disease and is not intended to
reflect the pathogenicity of the infectious agent. Historically, it has
been assumed that μ also represents the population’s crude birth rate,
thus ensuring that total population size does not change through time (dS/dt + dI/dt + dR/dt = 0).
This framework is very much geared toward the study of human infections
in developed nations—our approach would be different if the host
population exhibited its own “interesting” dynamics (as is often the
case with wildlife populations; see Chapter 5). Putting all these
assumptions together, we get the generalized SIR model:
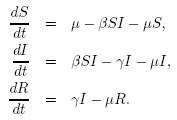
| μ |
is
the per capita death
rate, and the population level birth rate.
|
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| S(0) |
is
the initial
proportion of the population that are susceptible. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
Requirements.
All parameters must be positive, and S(0)+I(0) ≤ 1
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|


