|
Numerous infectious
diseases
are associated with a substantial
mortality risk. Examples include malaria, measles, whooping cough,
SARS, and dengue fever, among others. How do we explore the
consequences of infection-induced mortality? Specifically, how do we
incorporate a mortality probability into the SIR equations? The obvious approach
would be to add a term such as −mI
to the basic equation, where m
is a per capita disease-induced mortality rate for infected
individuals. However, this may be tricky to interpret biologically or
estimate from data. Instead, it is preferable to think about the
probability, ρ, of an
individual in the I class
dying from the infection before either recovering or dying from natural
causes.
We initial consider the case of density-dependent
transmission, where
as total population size N
decreases, due to disease-induced mortality, there is reduced
interaction between hosts. To make the dynamics clearer we switch to
considering the number or density (rather than proportion) of
individuals.
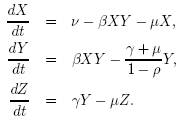
ρ
|
is
the mortality probability.
The probability than an infected individual dies from the disease
before recovering.
|
| μ |
is
the per capita death
rate from natural causes
|
| ν |
is
the population level
birth rate, we can equate ν/μ with the concept of a carrying capacity
|
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| X(0) |
is
the initial number or density of susceptible individuals. |
| Y(0) |
is
the initial number or density of infectious individuals. |
N(0)
|
is
the total population
size
|
All rates are
specified
in days.
Requirements.
All parameters must be positive. Remember, X, Y and ν all refer to numbers; ρ ≤ 1 as it is a probability.
Files
C++ Program, Python Program, Fortran Program, MATLAB Code.
|