|
An alternative approach that has been
tried in a variety of locations is pulse vaccination, where children in
certain age cohorts are periodically immunized. The principle aim of
pulse vaccination is to ensure the susceptible fraction is maintained
below this level by periodically immunizing a fraction of the
susceptible population. Pulse vaccination has gained in prominence as a
result of its highly successful application in the field. Compared to
“continual” pediatric vaccination, it has the additional advantage that
it is often logistically simpler to implement. A well-publicized
example is the spectacular control of poliomyelitis and measles in
Central and South America.
Here we assume that a proportion pV
of susceptible individuals are vaccinated every T time units (days):
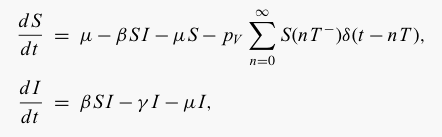
Again we allow for a delay, such that
vaccination is begun after time tV.
pV
|
is
the proportion of the susceptible individuals that are vaccinated with
each pulse.
|
T
|
is
the time between vaccination pulses.
|
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
ν
|
is the over-all birth set. We
set ν=μ to keep the population size
constant
|
μ
|
is the per captia death rate.
|
| tV |
is the time at which the
vaccination program is begun.
|
| S(0) |
is
the initial
proportion of the population that are susceptible. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
Requirements.
All parameters must be positive, S(0)+I(0) ≤ 1 and 0 ≤ pV ≤
1.
Files
Python Program, MATLAB Code.
|