|
We now consider a second extension to
the standard SIR model, introducing random vaccination at a rate v. Obviously vaccination only has
an impact on susceptible individuals (vaccination of infecteds and
recovereds is ineffective) and moves them into the recovered class.
This is an ideal model of the random vaccinaton of wildlife populations
where it is impossible to target the vaccination towards susceptible
individuals.
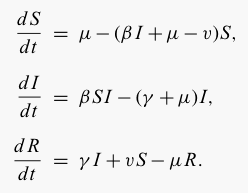
To allow a greater appreciation for
the impact of vaccination, the model is first integrated until time tV without vaccination (v=0) after which time the
vaccination campaign is begun.
v
|
is
the rate of random vaccination.
|
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
ν
|
is the over-all birth set. We
set ν=μ to keep the population size
constant
|
μ
|
is the per captia death rate.
|
| tV |
is the time at which the
vaccination program is begun.
|
| S(0) |
is
the initial
proportion of the population that are susceptible. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
Requirements.
All parameters must be positive, S(0)+I(0) ≤ 1.
Files
Python Program, MATLAB Code.
|


