Summary: A statistical theory of rogue waves is proposed and
tested against experimental data collected in a long water tank
where random waves with different degrees of nonlinearity are
mechanically generated and free to propagate along the
flume. Strong evidence is given that the rogue waves observed in
the tank are hydrodynamic instantons, that is, saddle
point configurations of the action associated with the stochastic
model of the wave system. As shown here, these hydrodynamic
instantons are complex spatio-temporal wave field configurations
which can be defined using the mathematical framework of Large
Deviation Theory and calculated via tailored numerical
methods. These results indicate that the instantons describe
equally well rogue waves that originate from a simple linear
superposition mechanism (in weakly nonlinear conditions) or from a
nonlinear focusing one (in strongly nonlinear conditions), paving
the way for the development of a unified explanation to rogue wave
formation.
Experimental Setup

The experimental data were recorded in the 270m long wave flume at
Marintek (Norway), schematically represented in the schematic. At one
end of the tank a plane-wave generator perturbs the water surface with
a predefined random signal, here taken to be the JONSWAP spectrum,
modelling a random sea state, with enhancement factor
\(\gamma\). These perturbations create long-crested wave trains that
propagate along the tank toward the opposite end, where they
eventually break on a smooth beach that suppresses most of the
reflections. The water surface \(\eta(x,t)\) is measured by probes
placed at different distances from the wave maker (\(x\)-coordinate).
The signal at the wave maker \(\eta(x=0,t) \equiv \eta_0(t)\) is
prepared according to the stationary random-phase statistics with
deterministic spectral amplitudes \(C(\omega_j)\). Experimental data
were collected for three different regimes: quasi-linear
(\(\gamma=1\), \(H_s=0.11\) m), intermediate (\(\gamma=3.3\),
\(H_s=0.13\) m), and highly nonlinear (\(\gamma=6\), \(H_s=0.15\) m).
Note that these three regimes have comparable significant wave
heights \(H_s\), but the difference in their enhancement
factors \(\gamma\) has significant dynamical consequences.
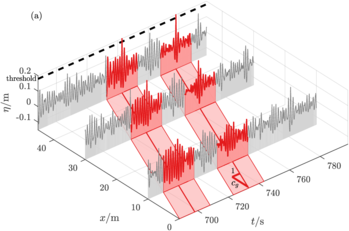
Extreme-event filtering: Extracting rogue waves from experimental data
To characterize the dynamics leading to extreme events of the water
surface, we adopt the following procedure: at a fixed location \(x=L\)
along the flume, we select small observation windows around all
temporal maxima of \(\eta\) that exceed a threshold \(z\). The choice of
the threshold \(z\) is meant to select extreme events with a similar
probability for all sets: the values of \(z=H_s=4\sigma\) for the
quasi-linear set, \(z=1.1\,H_s=4.4\sigma\) for the intermediate set and
\(z=1.2\,H_s=4.8\sigma\) for the highly-nonlinear set, where the maximum of the
surface elevation exceeds the threshold at the \(45\) m probe,
\(\eta(x=45\) m\(,t)\ge z\). We track the wave packet backward in space
and look at its shape at earlier points in the channel. This allows us
to build a collection of extreme events and monitor their
precursors.
Theoretical description of rogue waves via instantons of NLSE
To avoid solving fully nonlinear water wave equations that are
complicated from both theoretical and computational viewpoints, it is
customary to use simplified models such as the Nonlinear Schr\"odinger
equation (NLSE). If we exclude very nonlinear initial data, it is
known that NLSE captures the statistical properties of one dimensional
wave propagation to a good degree of accuracy up to a certain
time and it can be improved upon by using higher
order envelope equations. Because of their simplicity, NLSE and
extensions thereof have been successfully used to explain basics
mechanisms such as the modulational instability in water waves. With
the aim of capturing leading order effects, rather than describing the
full wave dynamics, here we restrict ourselves to the NLSE as a
prototype model for describing the nonlinear and dispersive waves in
the wave flume.
In the limit of deep-water, small-steepness, and
narrow-band properties, the evolution of the system is
described, to leading order in nonlinearity and dispersion, by the
one-dimensional NLSE:
$$
\frac{\partial \psi}{\partial x} + 2\frac{k_0}{\omega_0}
\frac{\partial \psi}{\partial t} + {i} \frac{k_0}{\omega_0^2}
\frac{\partial^2 \psi}{\partial t^2}+ 2 i {k_0^3} |\psi|^2\psi
= 0\,.
$$
The NLSE describes the change of the complex envelope \(\psi\equiv\psi(x,t)\)
that relates to the surface elevation via the Stokes series truncated
at second order:
$$
\eta = |\psi|\cos(\theta) + \tfrac12 k_0 |\psi|^2\cos(2\theta) +
O(k_0^2 |\psi|^3)\,,
$$
where \(\theta=k_0 x - \omega_0 t + \beta\) and \(\beta\) is the phase of
\(\psi\). In this expression the second order term can be neglected when
the field amplitude \(|\psi|\) is small — this is the case near the wave
maker at \(x=0\), where we will specify initial conditions for the
NLSE. However, this second order correction is
important when \(|\psi|\) becomes large, i.e. when rogue waves develop.
The NLSE is written as an evolution equation in space (rather than in
time) in order to facilitate the comparison with experimental data
which are taken along the spatial extend of the flume. Consistent
with the wave generator located at \(x=0\), we specify
\(\psi(x=0,t)=\psi_0(t)\) as initial condition for the NLSE, which we
take to be a Gaussian random field with a covariance whose Fourier
transform is related to the JONSWAP spectrum.
Large Deviation Theory and Instanton Calculus
Our analytical and computational descriptions of rare events rely on
instanton theory. Developed originally in the context of quantum
field theory, at its core lies the realization that the evolution of
any stochastic system, be it quantum and classical, reduces to a
well-defined (semi-classical) limit in the presence of a small
parameter. Concretely, the simultaneous evaluation of all possible
realizations of the system subject to a given constraint results in a
(classical or path-) integral whose integrand contains an action
functional \(S(\psi)\). The dominating realization can then be obtained
by approximating the integral by its saddle point approximation,
using the solution to \(\delta S(\psi^*)/\delta \psi=0\). This critical
point \(\psi^*\) of the action functional is called the instanton, and
it yields the maximum likelihood realization of the event. This
conclusion can also be justified mathematically within Large Deviation
Theory.
Specifically, we are interested in the probability
$$
P_L(z) \equiv \mathbb{P}(\eta(L,0)\ge z)
$$
i.e. the probability of the surface elevation at position \(L\) at an
arbitrary time \(t=0\) exceeding a threshold \(z\). This probability can
in principle be obtained by integrating the distribution of the
initial conditions over the set
$$
\Lambda(z)=\{\psi_0: \eta(L,0))\ge z\},\label{eq:13}
$$
i.e. the set of all initial conditions \(\psi_0\) at the wave maker
\(x=0\) that exceed the threshold \(z\) further down the flume at
\(x=L\). Since the initial field \(\psi_0(t)\) is Gaussian, the probability \(P_L(z)\) can therefore be
formally written as the path integral
$$
P_L(z) = Z^{-1} \int_{\Lambda(z)} \exp(-\tfrac12 \|\psi_0\|^2_C)\,D[\psi_0]\,,
$$
where \(Z\) is a normalization constant and the \(C\)-norm is induced by
the energy spectrum (in this case, JONSWAP) of the initial condition.
The set
\(\Lambda(z)\) has a very complicated shape in
general, that depends non-trivially on the nonlinear dynamics
of the NLSE since it involves the field at \(x=L>0\) down the
flume rather than \(x=0\). One way around this difficulty is to
estimate the integral via Laplace's
method. This strategy is the essence of Large deviation theory
(LDT), or, equivalently, instanton calculus, and it is
justified for large \(z\), when the probability of the set \(\Lambda(z)\)
is dominated by a single \(\psi_0\) contributing most to the integral. The optimal
condition leads to the constrained minimization problem
$$
\tfrac12\min_{\psi_0\in \Lambda(z)}\, \| \psi_0\|^2_C\equiv I_L(z)\,,
$$
and gives the large deviation estimate for \(P_L(z)\) of,
$$ P_L(z) \asymp \exp\left(-I_L (z) \right)\,,$$
where the symbol \(\asymp\) means asymptotic logarithmic equivalence,
i.e. the ratio of the logarithms of the two sides tends to 1 as
\(z\to\infty\), or, in other words, the exponential portion of both
sides scales in the same way with \(z\). Intuitively, this
estimate says that, in the limit of extremely strong (and
unlikely) waves, their probability is dominated by their least
unlikely realization, the instanton.
Now, the stochastic sampling problem is replaced by a deterministic
optimization problem, which we solve numerically. The trajectory
initiated from the minimizer \(\psi_0^*\) of the action will be referred
to as the instanton trajectory, and in the following we compare it
to trajectories obtained from the experiment.
Experimental Rogue Waves compared to Instantons
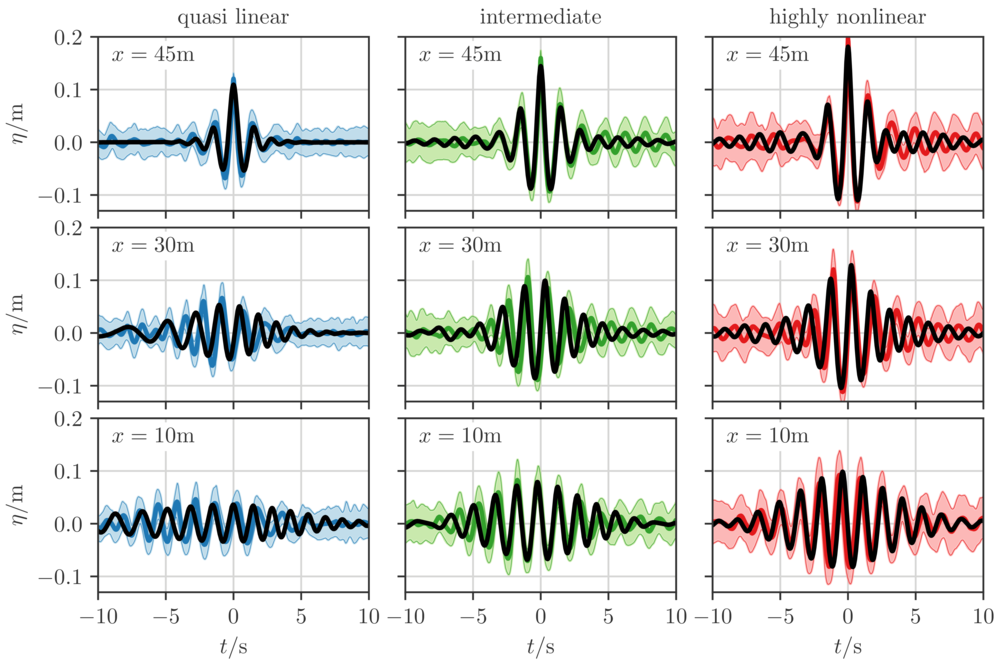
In the figure above, numerically computed instanton realizations are
depicted in solid black, while experimental averages and their
standard deviation are in color. We compare the evolution of rogue
waves observed in the experiment and averaged over many realizations
to that of the instanton, both constrained at \(x=45\) m. In all cases
the instanton tracks the dynamics of the averaged wave very closely
during the whole evolution. Moreover, in the focusing region the
standard deviation around the mean is small, especially toward the end
of the evolution. This observation in itself is a statement that
indeed all of the rogue waves such that \(\eta(L,0)\ge z\) resemble the
instanton plus small random fluctuations. The instanton approximation
shows excellent agreement not only across different degrees of
nonlinearity (and therefore substantially different physical
mechanisms), but also captures the behavior of precursors earlier
along the channel.
It is worth stressing that the instanton approach captures both the
linear and the fully nonlinear cases, unlike previous theories that
could describe each of these regimes individually but not both. To
make that point, in the next two sections we compare the predictions of
our approach to those of the quasi-determinism and semi-classical
theories that hold in the dispersive and nonlinear regimes,
respectively.
Conclusion
Here we have proposed a unifying framework based on Large Deviation
Theory and Instanton Calculus that is capable to describe with the
same accuracy the shape of rogue waves that result either from a
linear superposition or a nonlinear focusing mechanism. In the limit
of large nonlinearity, the instantons closely resemble the Peregrine
soliton to describe extreme events, but with the added bonus that our
framework predicts their likelihood; in the limit of linear waves, the
instanton reduces to the autocorrelation function. A smooth transition
between the two limiting regimes is also observed, and these
predictions are fully supported by experiments performed in a large
wave tank with different degrees of nonlinearity. These results were
obtained for one dimensional propagation, but there are no obstacles
to apply the approach to two horizontal dimensions, which may finally
explain the origin and shape of rogue waves in different setups,
including the ocean.
Relevant publications
-
G. Dematteis, T. Grafke, M. Onorato, and E. Vanden-Eijnden,
"Experimental Evidence of Hydrodynamic Instantons: The Universal Route to Rogue Waves",
Phys. Rev. X 9 (2019), 041057
-
G. Dematteis, T. Grafke, and E. Vanden-Eijnden,
"Extreme event quantification in dynamical systems with random components",
J. Uncertainty Quantification 7 (2019), 1029
-
G. Dematteis, T. Grafke, and E. Vanden-Eijnden,
"Rogue Waves and Large Deviations in Deep Sea",
PNAS 115 (2018), 855-860
-
T. Grafke, R. Grauer, and T. Schäfer, "The Instanton Method and
its Numerical Implementation in Fluid
Mechanics",
J. Phys. A: Math. Theor. 48 (2015), 333001