|
In this chapter we are primarily
concerned with the basic concept of control; how can control measures
be efficiently applied so as to minimise prevelance, minimise the
incidence of disease or even to erradicate infection all together.
We begin with a simple extension to the standard SIR model, including
prophylactic vaccination of new borne individuals. This form of control
simply 'moves' a proportion p
of new-bornes into the recovered (vaccinated) class rather than into
the susceptible class:
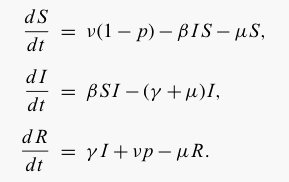
To allow a greater appreciation for
the impact of vaccination, the model is first integrated until time tV without vaccination (p=0) after which time the
vaccination campaign is begun.
p
|
is
the proportion of new-borne individuals who are vaccinated.
|
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
ν
|
is the over-all birth set. We
set ν=μ to keep the population size
constant
|
μ
|
is the per captia death rate.
|
| tV |
is the time at which the
vaccination program is begun.
|
| S(0) |
is
the initial
proportion of the population that are susceptible. |
| I(0) |
is
the initial
proportion of the population that are infectious. |
All rates are
specified
in days.
Requirements.
All parameters must be positive, S(0)+I(0) ≤ 1 and 0 ≤ p ≤ 1.
Files
Python Program, MATLAB Code.
|


