
|
Individual-based models can encompass
a wide range of model forms, and can be designed to include a variety
of complex and detailed host behavior that could not be readily
expressed within the other model types. As the name suggests, these
models consider the dynamics of individuals that occupy a spatial
landscape. As an additional example, we extend the SIR model (program
7.5) to the specific case of foot-and-mouth infection in the UK.
In this example, farms are the individual units and the transmission
kernal is given by a polynomial function that fits the data. Each farm
has an associated number of cattle and sheep which determine its
susceptiblity to infection and the rate that it transmits infection
once infectious. The rate at which a susceptible farm is infected is
given by:
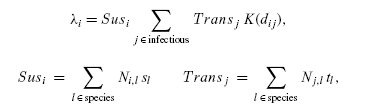
where the sum is over all infectious
individuals (labelled j), dij is the distance
between individuals i and j, and KT
is the transmission kernel. Sus
and Trans measure the
susceptiblity and transmissibility of individual farms, governed by the
number of livestock of each species Ni,l
and the species specific characteristics. Ni,l is log-normally
distributed to match the UK livestock census data.
In order to capture more realism, the infectious status of farms is
assumed to be determined by the time since infection; hence farms spend
exactly 5 days in the exposed class and 6 days in the infectious class.
Farms report infection on day 10 and are culled on day 12; on day 13
ring culling around infected farms takes place.
Parameters
Size
|
is
the length of the 2-D square
in which simulations take place, measured in kilometers
|
N
|
is
the population size, randomly distributed in 2-D
|
sl
|
is the susceptiblity of species l. ssheep = 1, scow = 10.5
|
tl
|
is
the transmissiblity of species l.
tsheep = 5.1
× 10-7, tcow
= 7.7 × 10-7 |
Ring
|
is
the size of the ring cull (in km) around each reported farm.
|
Y(0)
|
is
the number of initially infected individuals |
All rates are
specified
in days.
Requirements.
All parameters must be positive.
Files
MATLAB Code.
|
|


