Individual-based models can encompass
a wide range of model forms, and can be designed to include a variety
of complex and detailed host behavior that could not be readily
expressed within the other model types. As the name suggests, these
models consider the dynamics of individuals that occupy a spatial
landscape. Here, as an example of this methodology, we formulate a
general stochastic individual-based model based on the simple SIR model
in which only two events are possible: recovery which occurs at rate
γ
for any infected individual and transmission which is a spatial
process. The rate of transmission (or force of infection) to a
susceptible individual,
i, is
given by:
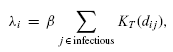
where the sum is over all infectious
individuals (labelled j), dij is the distance
between individuals i and j, and KT
is the transmission kernel. In these programs the kernel is a power-law
decay: KT(d) = d-α


