|
We now expand the approach used in
program 6.3 to implement event-driven stochasticity into the standard
SIR equations. There are now six different possible events which we
have to consider:
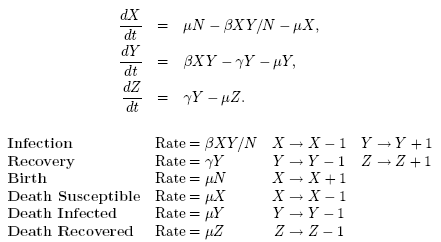
Once again we assume that the
population size N is constant
which prevents the permanent extinction of the host population.
Note that we are using numbers
(X,Y,Z) throughout this chapter for greater clarity.
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| μ |
is
the per capita death
rate.
|
| X(0) |
is
the initial number or density of susceptible individuals. |
| Y(0) |
is
the initial number or density of infectious individuals. |
N
|
is
the population
size -- assumed to be constant. We assume Z(0)=N-X(0)-Y(0)
|
All
rates are
specified
in days.
Requirements.
All parameters must be positive. Remember, X, Y, Z and N all refer to integer
numbers.
Files
Python Program, MATLAB Code.
|


