|
An intuitive way to incorporate noise
is to introduce it directly into the deterministic equations. As such,
the dynamics at each point in time are subject to some random
variability and this variability is propagated forward in time by the
underlying equations. We are, therefore, concerned with the interplay
between deterministic and stochastic forces—how they cancel out or
amplify each other.
In the previous example (program 6.1) noise was only applied to the
transmission term and its magnitude was set as an external parameter.
We now seek a more realistic formulation by making two changes to this
basic formulation:
1) a noise term is included for each of the six possible processes
(birth, infections, death of susceptibles, recovery, death of
infecteds, death of recovereds).
2) the magnitude of this noise term is a function of the rate of each
process. This is implemented by assuming events are Poisson distributed
such that the standard deviation of the noise scales with the
square-root of the mean.
The basic equations, assuming frequency-dependent
(mass-action) transmission, are transformed to:
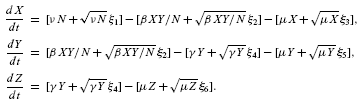
Note that we are using numbers
(X,Y,Z) throughout this
chapter for greater clarity.
| β |
is the transmission
rate and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
ξi
|
a
set of six noise
terms which are generated as a function of the time step.
|
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| μ |
is
the per capita death
rate.
|
νN
|
is
the birth rate, which is assumed to be constant and equal to μN; therefore preventing extinction
of the host population.
|
| X(0) |
is
the initial number or density of susceptible individuals. |
| Y(0) |
is
the initial number or density of infectious individuals. |
N
|
is
the population
size -- assumed to be constant.
|
All rates are
specified
in days.
Requirements.
All parameters must be positive. Remember, X, Y and N all refer to numbers.
A time step δt also has to be defined and this sets both the
integration step and scales the noise term ξ.
Files
Python Program, MATLAB Code.
|