|
It is now possible to extend the
formulation developed for the risk-structured SIS models to an
age-structured SIR model. This involves three major changes:
1) Given that we are now dealling with an SIR model, (at least) two
compartments need to be modelled per age group. (In fact we
should model S, I and R in each age-group and then use
the fact that the sum of all the population compartments equals 1 to
eliminate one of the variables. However, by assuming that the size each
of the age-classes (nC and nA) is at equilbrium,
we can simplify the dynamics and just consider two variable per
age-group.)
2) Demography needs to be included, this essentially means that
individuals need to be born into the youngest age-group. In addtion,
natural mortality can be age-structured.
3) Finally, individuals move through the age-classes as they mature. In
the two age-class example below individuals leave the childhood class
and move into the adult class, taking their infectious state with them.
In this set of programs we consider the simplest case where just two
age-groups (children and adults) are models. Again we use a
frequentist, such that SC, IC and RC
refer to the proportion of the entire population that are
susceptible, infectious or recovered and also in the childhood
age-class. Putting these elements together, we
arrive at the following differential equations:
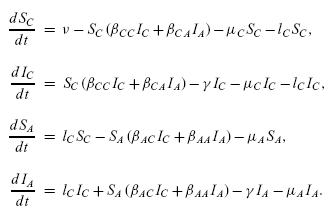
| β |
is the matrix of transmission
rates and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| lC |
is
the rate at which children mature and move into the adult age class
|
| nC |
is
the
proportion of the population that are in the childhood group. This is
not defined explicitly but calculated as: nC = μA/(lC+μA)
|
| μC |
is
the death rate in the childhood group
|
| μA |
is
the death rate in the adult group
|
| ν |
is
the birth rate into the childhood class. This is not defined explicitly
but calculated as: ν = (lC+μA) nC |
| SC(0) |
is
the initial
proportion of the population that are both susceptible and in the
childhood group. |
| IC(0) |
is
the initial
proportion of the population that are both infectious and in the
childhood group.
|
| SA(0) |
is
the initial
proportion of the population that are both susceptible and in the adult
group |
| IA(0) |
is
the initial
proportion of the population that are both infectious and in the adult
group. |
All rates are
specified
in years.
Requirements.
All parameters must be positive,
SC(0) + IC(0)≤
nC, and SA(0)
+ IA(0)≤
nA = 1- nC
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|