|
We start Chapter 3 by
considering the dynamics of an SIS-type infection in a population that
can be structured into a high-risk and a low-risk group. Focussing
initially on the behavior of the high-risk group, and denote the number
of susceptible and infectious individuals within this group by XH
and YH , and the total number in the high-risk group by NH
(=XH +YH ). Alternatively, it is often simpler to
use a frequentist approach, such that SH and IH
refer to the proportion of the entire population that are susceptible
or infectious and also in the high-risk group, in which case nH
is the proportion of the population in the high-risk group: SH
= XH/N, IH = YH/N, nH = NH/N.
The dynamics of either group is derived from two basic events,
infection and recovery. We initially focus on the dynamics of the
high-risk group. Recovery, or the loss of infectious cases, can occur
only through treatment and, following the unstructured formulation, we
assume this occurs at a constant rate γ . New infectious cases within
the high-risk group occur when a high-risk susceptible is infected by
someone in either the high- or low-risk group. These two distinct
transmission types require different transmission parameters: We let βHH
denote transmission to high risk from high-risk and βHL
represent transmission to high risk from low risk. (Note throughout
this book we use the same ordering of subscripts such that transmission
is always βto from) Putting these elements together, we
arrive at the following differential equations:
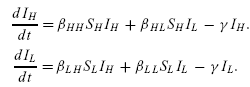
| β |
is the matrix of transmission
rates and incorporates the encounter rate between susceptible and
infectious individuals together with the probability of transmission. |
| γ |
is
called the removal
or recovery rate, though often we are more interested in its reciprocal
(1/γ) which determines the average infectious period. |
| nH |
is
the
proportion of the population that are in the high risk group
|
| IH(0) |
is
the initial
proportion of the population that are both infectious and in the high
risk group. |
| IL(0) |
is
the initial
proportion of the population that are both infectious and in the low
risk group.
|
All rates are
specified
in years.
Requirements.
All parameters must be positive, and nH ≤ 1, IH(0)≤
nH, IL(0)≤
1-nH,
Files
C++ Program, Python Program, Fortran Program, Parameters, MATLAB Code.
|


