Tobias Grafke — Rogue Waves and Large Deviations

Summary: A statistical theory of rogue waves is proposed and tested against experimental data collected in a long water tank where random waves with different degrees of nonlinearity are mechanically generated and free to propagate along the flume. Strong evidence is given that the rogue waves observed in the tank are hydrodynamic instantons, that is, saddle point configurations of the action associated with the stochastic model of the wave system. As shown here, these hydrodynamic instantons are complex spatio-temporal wave field configurations which can be defined using the mathematical framework of Large Deviation Theory and calculated via tailored numerical methods. These results indicate that the instantons describe equally well rogue waves that originate from a simple linear superposition mechanism (in weakly nonlinear conditions) or from a nonlinear focusing one (in strongly nonlinear conditions), paving the way for the development of a unified explanation to rogue wave formation.

Experimental Setup

The experimental data were recorded in the 270m long wave flume at Marintek (Norway), schematically represented in the schematic. At one end of the tank a plane-wave generator perturbs the water surface with a predefined random signal, here taken to be the JONSWAP spectrum, modelling a random sea state, with enhancement factor $\gamma$. These perturbations create long-crested wave trains that propagate along the tank toward the opposite end, where they eventually break on a smooth beach that suppresses most of the reflections. The water surface $\eta(x,t)$ is measured by probes placed at different distances from the wave maker ($x$-coordinate). The signal at the wave maker $\eta(x=0,t) \equiv \eta_0(t)$ is prepared according to the stationary random-phase statistics with deterministic spectral amplitudes $C(\omega_j)$. Experimental data were collected for three different regimes: quasi-linear ($\gamma=1$, $H_s=0.11$ m), intermediate ($\gamma=3.3$, $H_s=0.13$ m), and highly nonlinear ($\gamma=6$, $H_s=0.15$ m). Note that these three regimes have comparable significant wave heights $H_s$, but the difference in their enhancement factors $\gamma$ has significant dynamical consequences.

Extreme-event filtering: Extracting rogue waves from experimental data

To characterize the dynamics leading to extreme events of the water surface, we adopt the following procedure: at a fixed location $x=L$ along the flume, we select small observation windows around all temporal maxima of $\eta$ that exceed a threshold $z$. The choice of the threshold $z$ is meant to select extreme events with a similar probability for all sets: the values of $z=H_s=4\sigma$ for the quasi-linear set, $z=1.1\,H_s=4.4\sigma$ for the intermediate set and $z=1.2\,H_s=4.8\sigma$ for the highly-nonlinear set, where the maximum of the surface elevation exceeds the threshold at the $45$ m probe, $\eta(x=45$ m$,t)\ge z$. We track the wave packet backward in space and look at its shape at earlier points in the channel. This allows us to build a collection of extreme events and monitor their precursors.

Theoretical description of rogue waves via instantons of NLSE

To avoid solving fully nonlinear water wave equations that are complicated from both theoretical and computational viewpoints, it is customary to use simplified models such as the Nonlinear Schr\"odinger equation (NLSE). If we exclude very nonlinear initial data, it is known that NLSE captures the statistical properties of one dimensional wave propagation to a good degree of accuracy up to a certain time and it can be improved upon by using higher order envelope equations. Because of their simplicity, NLSE and extensions thereof have been successfully used to explain basics mechanisms such as the modulational instability in water waves. With the aim of capturing leading order effects, rather than describing the full wave dynamics, here we restrict ourselves to the NLSE as a prototype model for describing the nonlinear and dispersive waves in the wave flume.

In the limit of deep-water, small-steepness, and narrow-band properties, the evolution of the system is described, to leading order in nonlinearity and dispersion, by the one-dimensional NLSE:

$$ \frac{\partial \psi}{\partial x} + 2\frac{k_0}{\omega_0} \frac{\partial \psi}{\partial t} + {i} \frac{k_0}{\omega_0^2} \frac{\partial^2 \psi}{\partial t^2}+ 2 i {k_0^3} |\psi|^2\psi = 0\,. $$

The NLSE describes the change of the complex envelope $\psi\equiv\psi(x,t)$ that relates to the surface elevation via the Stokes series truncated at second order:

$$ \eta = |\psi|\cos(\theta) + \tfrac12 k_0 |\psi|^2\cos(2\theta) + O(k_0^2 |\psi|^3)\,, $$

where $\theta=k_0 x - \omega_0 t + \beta$ and $\beta$ is the phase of $\psi$. In this expression the second order term can be neglected when the field amplitude $|\psi|$ is small — this is the case near the wave maker at $x=0$, where we will specify initial conditions for the NLSE. However, this second order correction is important when $|\psi|$ becomes large, i.e. when rogue waves develop.

The NLSE is written as an evolution equation in space (rather than in time) in order to facilitate the comparison with experimental data which are taken along the spatial extend of the flume. Consistent with the wave generator located at $x=0$, we specify $\psi(x=0,t)=\psi_0(t)$ as initial condition for the NLSE, which we take to be a Gaussian random field with a covariance whose Fourier transform is related to the JONSWAP spectrum.

Large Deviation Theory and Instanton Calculus

Our analytical and computational descriptions of rare events rely on instanton theory. Developed originally in the context of quantum field theory, at its core lies the realization that the evolution of any stochastic system, be it quantum and classical, reduces to a well-defined (semi-classical) limit in the presence of a small parameter. Concretely, the simultaneous evaluation of all possible realizations of the system subject to a given constraint results in a (classical or path-) integral whose integrand contains an action functional $S(\psi)$. The dominating realization can then be obtained by approximating the integral by its saddle point approximation, using the solution to $\delta S(\psi^*)/\delta \psi=0$. This critical point $\psi^*$ of the action functional is called the instanton, and it yields the maximum likelihood realization of the event. This conclusion can also be justified mathematically within Large Deviation Theory.

Specifically, we are interested in the probability

$$ P_L(z) \equiv \mathbb{P}(\eta(L,0)\ge z) $$

i.e. the probability of the surface elevation at position $L$ at an arbitrary time $t=0$ exceeding a threshold $z$. This probability can in principle be obtained by integrating the distribution of the initial conditions over the set

$$ \Lambda(z)=\{\psi_0: \eta(L,0))\ge z\},\label{eq:13} $$

i.e. the set of all initial conditions $\psi_0$ at the wave maker $x=0$ that exceed the threshold $z$ further down the flume at $x=L$. Since the initial field $\psi_0(t)$ is Gaussian, the probability $P_L(z)$ can therefore be formally written as the path integral

$$ P_L(z) = Z^{-1} \int_{\Lambda(z)} \exp(-\tfrac12 \|\psi_0\|^2_C)\,D[\psi_0]\,, $$

where $Z$ is a normalization constant and the $C$-norm is induced by the energy spectrum (in this case, JONSWAP) of the initial condition. The set $\Lambda(z)$ has a very complicated shape in general, that depends non-trivially on the nonlinear dynamics of the NLSE since it involves the field at $x=L>0$ down the flume rather than $x=0$. One way around this difficulty is to estimate the integral via Laplace's method. This strategy is the essence of Large deviation theory (LDT), or, equivalently, instanton calculus, and it is justified for large $z$, when the probability of the set $\Lambda(z)$ is dominated by a single $\psi_0$ contributing most to the integral. The optimal condition leads to the constrained minimization problem

$$ \tfrac12\min_{\psi_0\in \Lambda(z)}\, \| \psi_0\|^2_C\equiv I_L(z)\,, $$

and gives the large deviation estimate for $P_L(z)$ of,

$$ P_L(z) \asymp \exp\left(-I_L (z) \right)\,,$$

where the symbol $\asymp$ means asymptotic logarithmic equivalence, i.e. the ratio of the logarithms of the two sides tends to 1 as $z\to\infty$, or, in other words, the exponential portion of both sides scales in the same way with $z$. Intuitively, this estimate says that, in the limit of extremely strong (and unlikely) waves, their probability is dominated by their least unlikely realization, the instanton.

Now, the stochastic sampling problem is replaced by a deterministic optimization problem, which we solve numerically. The trajectory initiated from the minimizer $\psi_0^*$ of the action will be referred to as the instanton trajectory, and in the following we compare it to trajectories obtained from the experiment.

Experimental Rogue Waves compared to Instantons

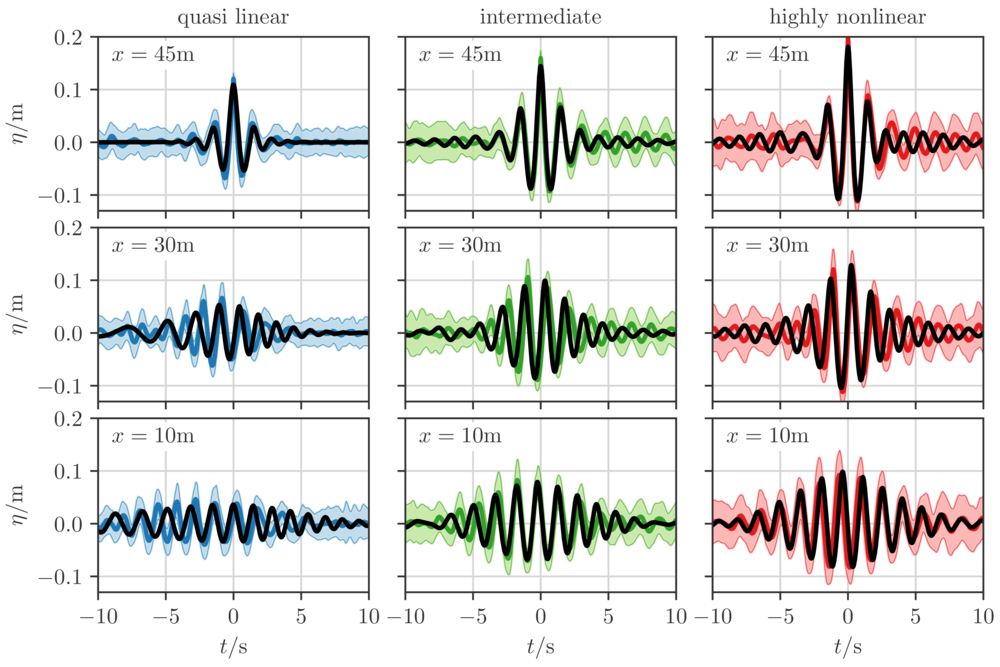
In the figure above, numerically computed instanton realizations are depicted in solid black, while experimental averages and their standard deviation are in color. We compare the evolution of rogue waves observed in the experiment and averaged over many realizations to that of the instanton, both constrained at $x=45$ m. In all cases the instanton tracks the dynamics of the averaged wave very closely during the whole evolution. Moreover, in the focusing region the standard deviation around the mean is small, especially toward the end of the evolution. This observation in itself is a statement that indeed all of the rogue waves such that $\eta(L,0)\ge z$ resemble the instanton plus small random fluctuations. The instanton approximation shows excellent agreement not only across different degrees of nonlinearity (and therefore substantially different physical mechanisms), but also captures the behavior of precursors earlier along the channel.

It is worth stressing that the instanton approach captures both the linear and the fully nonlinear cases, unlike previous theories that could describe each of these regimes individually but not both. To make that point, in the next two sections we compare the predictions of our approach to those of the quasi-determinism and semi-classical theories that hold in the dispersive and nonlinear regimes, respectively.

Conclusion

Here we have proposed a unifying framework based on Large Deviation Theory and Instanton Calculus that is capable to describe with the same accuracy the shape of rogue waves that result either from a linear superposition or a nonlinear focusing mechanism. In the limit of large nonlinearity, the instantons closely resemble the Peregrine soliton to describe extreme events, but with the added bonus that our framework predicts their likelihood; in the limit of linear waves, the instanton reduces to the autocorrelation function. A smooth transition between the two limiting regimes is also observed, and these predictions are fully supported by experiments performed in a large wave tank with different degrees of nonlinearity. These results were obtained for one dimensional propagation, but there are no obstacles to apply the approach to two horizontal dimensions, which may finally explain the origin and shape of rogue waves in different setups, including the ocean.

Relevant publications

G. Dematteis, T. Grafke, M. Onorato, and E. Vanden-Eijnden, "Experimental Evidence of Hydrodynamic Instantons: The Universal Route to Rogue Waves", Phys. Rev. X 9 (2019), 041057
G. Dematteis, T. Grafke, and E. Vanden-Eijnden, "Extreme event quantification in dynamical systems with random components", J. Uncertainty Quantification 7 (2019), 1029
G. Dematteis, T. Grafke, and E. Vanden-Eijnden, "Rogue Waves and Large Deviations in Deep Sea", PNAS 115 (2018), 855-860
T. Grafke, R. Grauer, and T. Schäfer, "The Instanton Method and its Numerical Implementation in Fluid Mechanics", J. Phys. A: Math. Theor. 48 (2015), 333001