
Wave Turbulence

| Waves are everywhere. They are seen at all scales, from quantum to cosmological, and in many natural and astrophysical contexts. While they are produced by a vast variety of physical forces, they have a common core of mathematical descriptions. They often occur in random ensembles such as on a sea surface stirred by a recent storm. The Wave Turbulence description addresses the long time, chaotic behaviours of a sea of weakly coupled dispersive wavetrains in the presence of sources and sinks. The subject is remarkably rich. It has a wealth of applications from oceans to atmospheres, from the solar wind to semiconductor lasers. It provides a most tractable example of a non-equilibrium statistical system. It has undergone a recent resurgence driven by its enormous applications potential, its role as a natural paradigm for non-equilibrium systems and by some new discoveries connected with intermittency and the random occurrence of coherent events. |
Astrophysical Turbulence

| Interstellar scintillation (ISS) is defined as the fluctuations in amplitude and phase of radio waves emitted by objects like pulsars. Origin of ISS is found in the scattering of radio waves by electron density fluctuations in the ionized interstellar medium whose power law spectrum extends from scales of the order of 1.e9m to the scale of the interstellar clouds itself (1.e17m). It is often assumed that the origin of the power law spectrum is due to turbulence but up to now there is no theory of interstellar turbulence. The ubiquitous presence of an interstellar magnetic field and its important dynamical role suggest that such a theory could be based on MHD equations. On the other hand, the anisotropic scattering of radio waves suggests that the electron density fluctuations are preferentially perpendicular to the mean magnetic field and therefore that a theory of interstellar turbulence could be built rigorously in the framework of wave turbulence. |
Turbulence in Bose-Einsten condensates
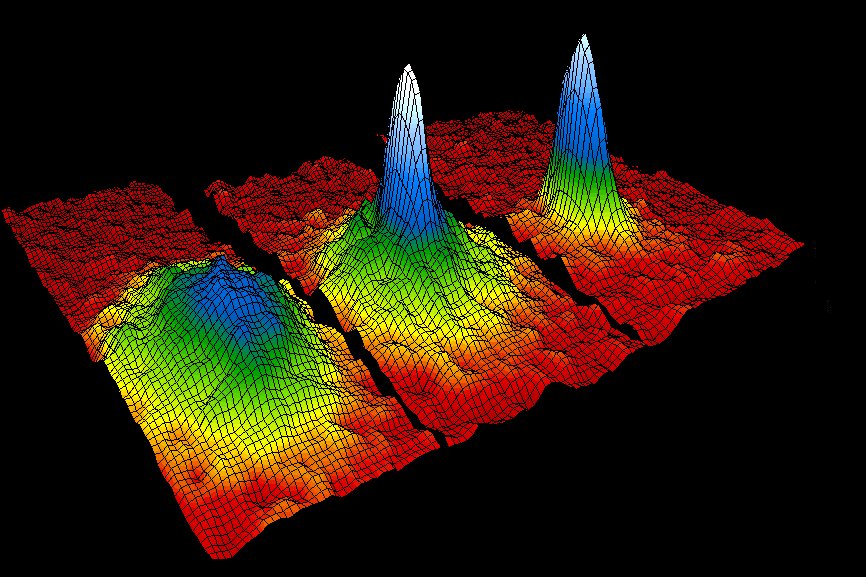
| Bose-Einstein condensate (BEC) was perdicted in 1924 but it was not until 1995 that it was discovered experimentally at the JILA lab in Boulder Colorado. This work was awarded by the 2001 Nobel Prize in physics and it lead to a resurgence of the theoretical studies of the BEC phenomenon. Basically, BEC is a state of super-cold matter where most of the gas atoms occupy the lowest possible energy level (see the picture insert which shows the JILA's experimental result about the energy concentration near the zero-momentum ground state). It is common in the low-temperature physics to describe gases by the thermodynamic theory in terms of temperatures and chemical potentials. However, this description becomes invalid when the system is far from equilibrium, and this turns out to be the case during the Bose condensation. Thermodynamic description here would be as un-realistic as a description of waterfalls using a theory developed for lakes. |
Navier-Stokes Turbulence
| Navier-Stokes turbulence, or simply turbulence in water and air, is the subject of study of a vast number of researchers in physics, mathematics and engineering. Some properties of turbulence are well established, for example persistent occurence of the energy cascade through scales or the exact form of the third order velocity correlator. However, there is much more about the NS turbulence that is not known, and to date there is no systematic statistical description of this phenomenon. Direct numerical simulations (DNS) using powerful modern computers come as great help in predicting turbulence. However, even the most powerful computers cannot resolve motion at small scales which contains nearly 90% of the turbulence energy in important atmospheric and oceanic applications and this situation is not likely to get better in near future solely due to increases in the computational power. Not everything can be done by brute force. |