Last changed Wed Aug 29 13:31:01 BST 2001
We are grateful to David Wright who produced a number of pictures in connection with our paper  inserttitle .
The current document was written by David Wright, to explain what he had done. His document has since been
lightly edited by David Epstein.  The original form of the document was produced using latex2html by Nikos Drakos.

The Trace $2\sqrt{2}$ slice

This is a study instigated by Epstein, Marden and Markovic into a slice related to bending-and-earthquake coordinates.

For downloading, the source of this document is in

TeX Document (tar.gz)
while the source of all related pictures (6.4 M) is in
Pictures etc.
The groups are defined by the matrices
\begin{displaymath}a= \begin{pmatrix}\sqrt{2} \, e^{z/2} & (1+\sqrt{2})\, e^{z......b=\begin{pmatrix}\sqrt2-1 & 0 \\ 0 & \sqrt 2 + 1 \end{pmatrix}\end{displaymath}


These correspond to traces

\begin{displaymath}\mathop{\text{Tr}}\nolimits a = 2\sqrt2 \cosh(z/2)\qquad\ma......mits b = 2\sqrt 2\qquad\mathop{\text{Tr}}\nolimits abAB = -2\end{displaymath}


(using the upper case convention for inverses).

We use a boundary tracing method for exploring the values of $\mathop{\text{Tr}}\nolimits a$for which such a group is discrete. The p/q word in a and b is defined by

\begin{displaymath}w_{0/1} = a\qquadw_{1/0} = B\qquadw_{(p+r)/(q+s)} = w_{p/q} w_{r/s} \text{for Farey neighbor fractions}\end{displaymath}


We solve in order of p/q for values of $\mathop{\text{Tr}}\nolimits a$ where wp/q has trace 2.

The resulting plot of $i\, \mathop{\text{Tr}}\nolimits a$ is below, for cusps ranging from -3/1 just off to the left to 3/1 just off to the right.

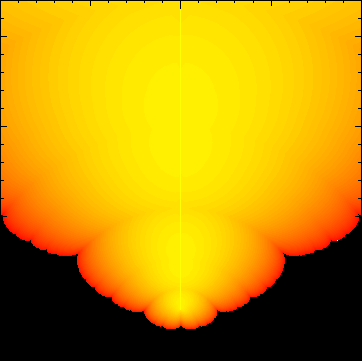
\epsfig{width=8cm,file=wright-pix/epstein-slice-clr.epsi}
The PostScript for this is at
epstein-slice-clr.epsi
Then we apply (in Maple) the map $z= 2 \,\text{arccosh}( \mathop{\text{Tr}}\nolimits a / (2\sqrt2))$ to the boundary values calculated above to get the slice in earthquake coordinates. This is below:
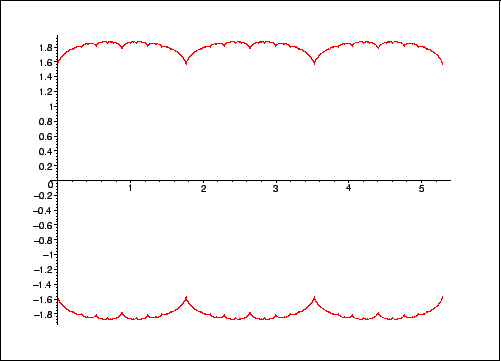
\epsfig{width=8cm,angle=270,file=wright-pix/epstein-maple.epsi}
The PostScript for this is at
epstein-maple.ps
We then computed the limit set for a point at the apparent ``maximum'' of the upper curve. This appears to be at the limit of the Fibonacci cusps Fn/Fn+1 as $n\to \infty$. The limit set is
\epsfig{width=8cm,file=wright-pix/epstein-lset.epsi}
The PostScript for this is at
epstein-lset.epsi


epstein-lset.epsi is a large file (around 30Mb). The advantage of taking a look at it with a PostScript viewer, like ghostscript or gv, is that David Wright's program computes the limit set in circular order. The limit set is naturally the continuous image of a circle. In the viewer, the picture appears comparatively slowly, and you see a movie of the image in the plane of a point on the circle. This enables one to see the map, rather than just the image of the map.