Next: Bibliography
The Moment Map:
Nonlinear Dynamics of Density Evolution Via a Few Moments
Dwight Barkley, Yannis Kevrekidis, Andrew Stuart
We explore situations in which certain stochastic and high-dimensional deterministic systems behave effectively as low-dimensional dynamical systems. We define and study moment maps, maps on spaces of low-order moments of evolving distributions, as a means of understanding equation-free multiscale algorithms for these systems. The moment map itself is deterministic and attempts to capture the implied probability distribution of the dynamics. By choosing situations where the low-dimensional dynamics can be understood a priori, we evaluate the moment map. Despite requiring the evolution of an ensemble to define the map, it can be an efficient numerical tool as the map opens up the possibility of bifurcation analyses and other high level tasks being performed on the system. We demonstrate how nonlinearity arises in these maps and how this results in the stabilization of metastable states. Examples are shown for a hierarchy of models, ranging from simple stochastic differential equations to molecular dynamics simulations of a particle in contact with a heat bath. Some relevant papers are [1,2,3,4,5] and references therein.
![]()
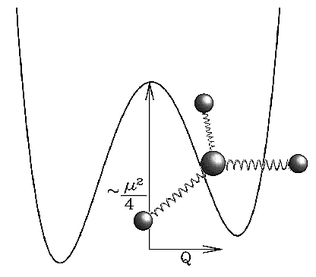
 The
systems we consider are exemplified by the following model. A
particle, called the distinguished particle, with position Q and
momentum P sits in a potential well V(Q). It is coupled via linear
springs to a large number of particles comprising a heat bath; see
left figure. The potential well considered here is a slightly
asymmetric double well. The dynamics of this simple model is typical
of many more complex molecular and stochastic systems in which the
state is primarily confined to a few conformations with rare
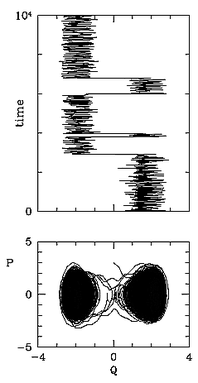
switching events between them. This is illustrated in right figure
with a typical trajectory and time series for the distinguished
particle. The system exhibits metastability.
The
systems we consider are exemplified by the following model. A
particle, called the distinguished particle, with position Q and
momentum P sits in a potential well V(Q). It is coupled via linear
springs to a large number of particles comprising a heat bath; see
left figure. The potential well considered here is a slightly
asymmetric double well. The dynamics of this simple model is typical
of many more complex molecular and stochastic systems in which the
state is primarily confined to a few conformations with rare
switching events between them. This is illustrated in right figure
with a typical trajectory and time series for the distinguished
particle. The system exhibits metastability.
We study the behavior of coarse dynamics and coarse bifurcation methods on problems which exhibit metastable behavior of this type.
![]()
Some movies of the Moment Map
|
In all cases: Blue denotes fixed points of the map. These are shown either as distributions (left half) or as fixed points in the phase plane (right half). Red denotes iterates of the map, generally on stable/unstable manifolds of saddle fixed points. Green shows the evolution of the microscopic system
In the first three cases, the underlying system in a one-variable SDE. In the last case the underlying system is a two-variable SDE.
The first-order moment map (top) is a 1D map on the mean <x>. Phase-space points correspond to delta distributions.
The second-order moment map (next two cases) is a 2D map on the mean and standard deviation (<x>, sigma). Phase-space points correspond to Gaussian distributions. Note the saddle fixed point corresponds to a wide distribution. The stable fixed points correspond to metastable measures in the well bottoms. The map stabilized metastable fixed points by introducing nonlinearity.
The final case is a second-order moment map for a two-dimensional SDE. The phase space of the moment map is five dimensional: 2 means, 2 standard deviations, and a cross correlation (<Q>, <P>, st(Q), st(P), corr). Points the the 5D phase space are represented naturally by ellipses. The movie shows a trajectory evolving from a representative initial condition towards one of the two stable fixed points.
|
Only the mean of the distribution is captured with the map. (movie 432Kb). |
|
The mean and the width of the distribution is captured by the map. Shown is a trajectory almost on one branch of the stable manifold of the saddle fixed point. The trajectory passes near the saddle and then to one of the two stable fixed points. (movie 725Kb). |
|
|
Same as above except trajectory starting nearly on the other branch of stable manifold. (movie 1.3Mb). |
|
|
Trajectory for the second order moment map including both position and momentum. (movie 1.8Mb). |
Next: Bibliography