|
Onset of vortex shedding |
|
Below the critical Reynolds number (Rec = 46) the flow past a circular cylinder is steady and reflection symmetric. (Shown to the left is vorticity and separating streamlines at Re=40) |
|
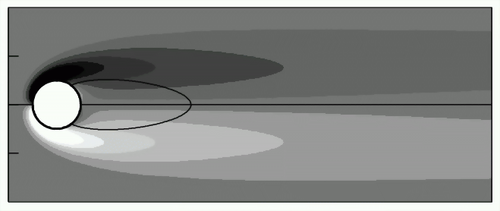
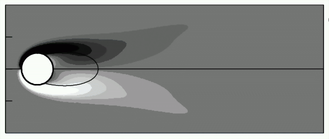
Above Rec the flow is time periodic. One observes the famous Benard-von-Kaman vortex street. (Shown to the left is a snapshot of the flow at Re=100) |
|
A large body of research has been devoted to understanding this curve. |
 Steady
Flow
Steady
Flow Vortex
shedding
Vortex
shedding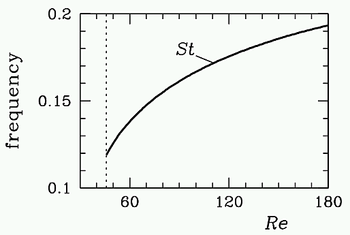 If
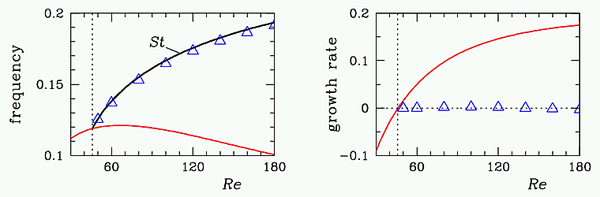
one measures, either in experiment or in numerical simulations,
the oscillation frequency as a function of Reynolds number, one
obtains the plot shown to the right. St
If
one measures, either in experiment or in numerical simulations,
the oscillation frequency as a function of Reynolds number, one
obtains the plot shown to the right. St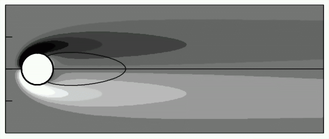

 Starting
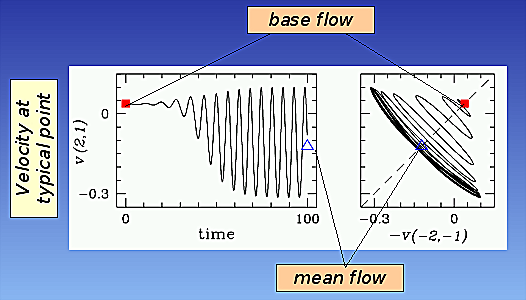
from the unstable base flow at Re=100, oscillations
develop. As they do, the mean changes and frequency increases.
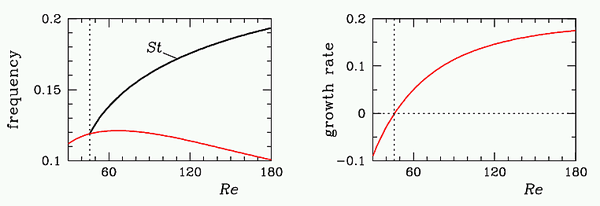
Starting
from the unstable base flow at Re=100, oscillations
develop. As they do, the mean changes and frequency increases.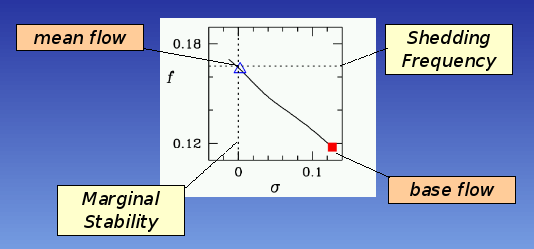 As
the flow evolves from the base flow, Reynolds stresses grow. As
they do the flow evolves to a point of marginal stability of
the mean flow, at which point the frequencies is the nonlinear
Strouhal number.
As
the flow evolves from the base flow, Reynolds stresses grow. As
they do the flow evolves to a point of marginal stability of
the mean flow, at which point the frequencies is the nonlinear
Strouhal number.