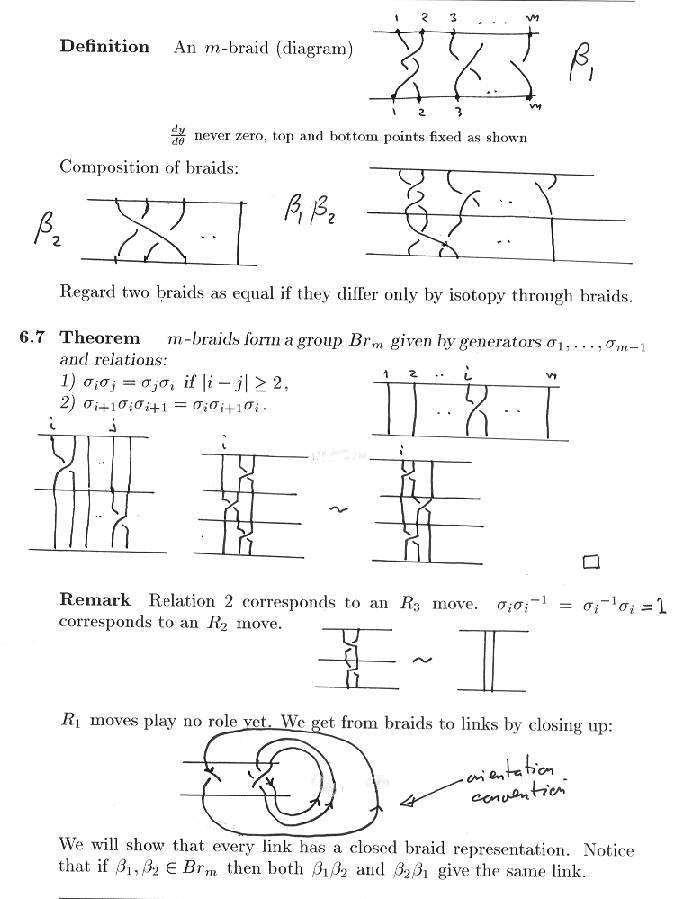

Proof The idea is to turn c's into a's by flyping. A flype moves a crossing across a part of a diagram at the expense of turning the part over:
Notice that if we introduce two crossings using R2 then move one over with a flype we get:
Suppose c > 0 and consider the sequence of flypes:
Repeat c times to get:
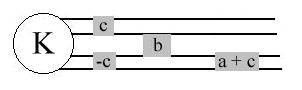
Similarly if c < 0 . If b
is
odd K will have been rotated through pi about an horizontal
axis.
Use this procedure to eliminate cn , cn-1 , ... ,c2
in turn. Then finally:


We can be more efficient in unwrapping a daisy chain. For example:

After n - 2 double flypes we have:

We now use flips to eliminate the unshaded crossings. Here is
a flip:

Think of this as turning R over to change the sign of a crossing
between
middle and outer string at the expense of adding a crossing between
middle
and other outer string.
Combine a flip with R2 to get 3 new crossings all of the same sign
as
follows:
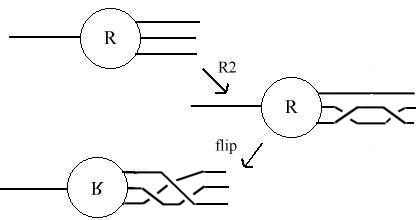
Apply R2 flips:


etc.
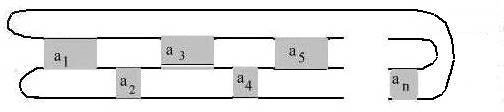
If n odd get:

which is isotopic to
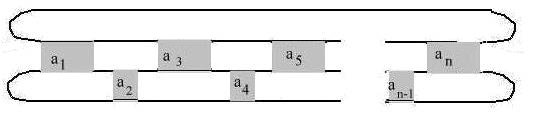
and if n even get:
which is isotopic to:
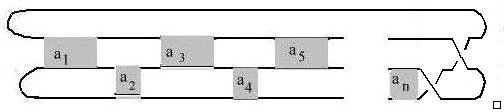
Remark It follows that the classes of knots defined by
Daisy chains, 4-plats and 2-bridge knots are identical.