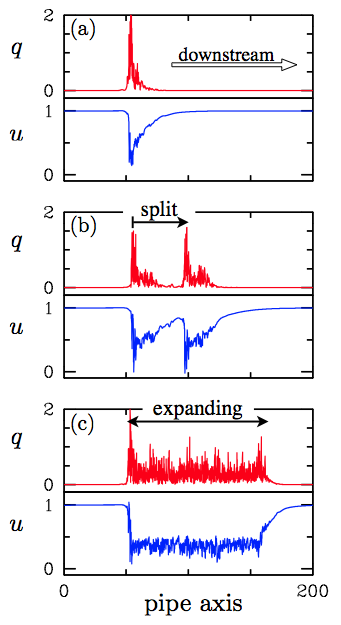
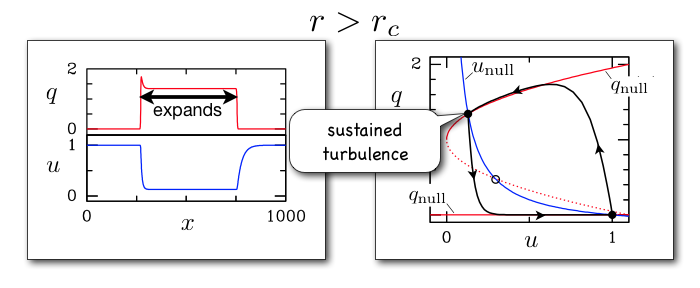
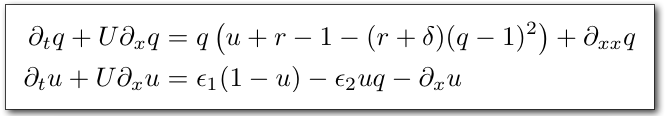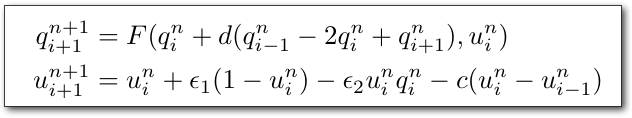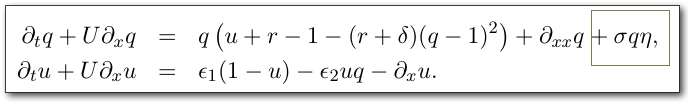-
Two Variables
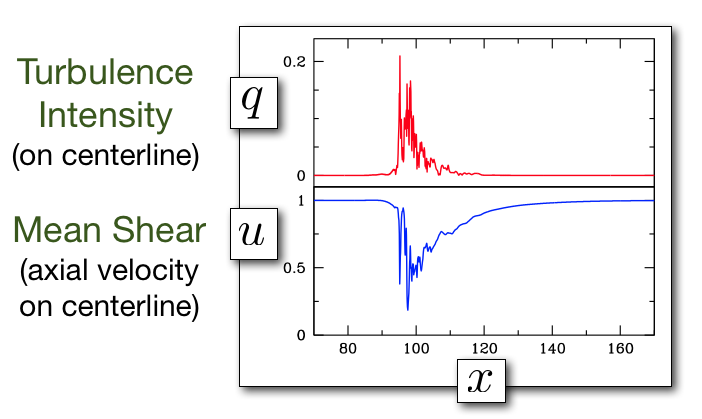
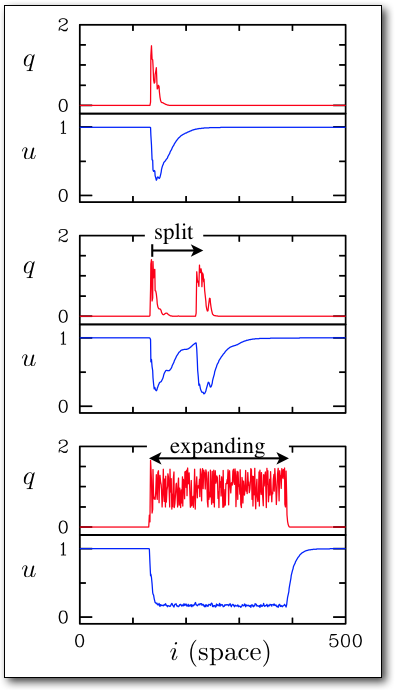
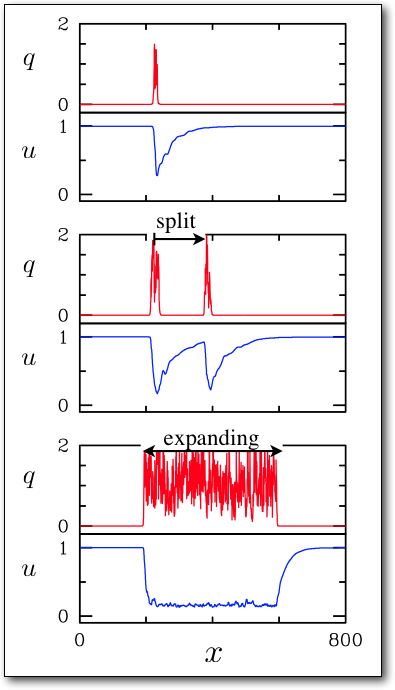
Shown below are the instantaneous turbulent fluctuations and the mean shear profiles from direct numerical simulation (DNS) of a turbulent puff at Re=2000. (The turbulent fluctuations are here simply the magnitude of transverse velocity. The mean is shear profiles are instantaneous azimuthal averages of streamwise velocity.)

Two scalar variables, q and u, depending only on streamwise coordinate x are obtained by sampling the above fields on the centerline. The axial velocity on the centerline provides a convenient proxy for the mean shear.